古希腊毕达哥拉斯学派(在古希腊哲学中毕达哥拉斯学派的中心思想是什么)
浅析希腊哲学之——毕达哥拉斯学派2
一方面,他在解释数是如何形成万事万物时,仍然会受自然哲学的影响,将数具象化,与形相互联系。他认为数是万物的本原,而1则是数的本原,这一点与老子的“一生二,二生三,三生万物”的观点很相近。

老子
并且作为本原的1以及由1构成的2、3、4等数都具有空间意义:1就是一个点,2就是两个点连成的一条直线,3则为三个点构成的一个面,4则是四个点构成的一个体,之后体再按照不同的排列方式构成水、火、土、气这四种最基本的自然物质,最终水、火、土、气再构成万事万物。
从这个角度来说,毕达哥拉斯其实是把作为万事万物本原的数理解为具有几何形状的东西,即点、线、面、体,或者是物理学意义上的数,也就是具有广延性(占有空间位置)的物质微粒。毕达哥拉斯这种“数本原说”与后来德谟克利特提出的“原子论”观点也有许多契合之处。

德谟克利特
另一方面,毕达哥拉斯又将数神秘化,将其说成是在事物背后起决定性作用、决定着事物性质的某种抽象物。
这样一来,数就成了万事万物背后的比例关系和抽象原则,就像希腊悲剧中在英雄背后起决定作用的命运那样的隐藏规则。
比如,毕达哥拉斯将1当成是真理,因为1是最基本的数;将2当成是意见,因为它摇摆不定;将4和9当成正义,因为4和9分别为第一个偶数2和第一个奇数3的平方(以毕达哥拉斯那里,1是作为本原的基本数,既不是奇数也不是偶数);
将5当成是婚姻,因为它是第一个偶数2和第一个奇数3的和;将10当成是圆满,因为它是1、2、3、4之和。这样一种带有隐喻或象征特点的哲学观点当然有一定的抽象意味,它表明了数量关系与事物性质之间的联系,同时也带有一种明显的、像巫术一样的神秘色彩。由此可以看出,在最初的抽象思维中,哲学与宗教是不分彼此地混合在一起的。
三、亚里士多德与“形而上学”“形而上学”来自希腊语,其写法为metaphysics。这是个复合词,其中“meta”指“在……之后”,现在是很多英语单词的前缀;“physics”的含义是“物理学”。古希腊时期,物理学的含义是非常广泛的,几乎所有自然科学都被称为物理学。

“meta”与“physics”合在一起,直译就是“在物理学之后”,后来翻译成中文时译为“形而上学”。“形而上学”这个概念出现得较晚,作为形而上学的先驱,尽管毕达哥拉斯的抽象思维中已经具备了形而上学的思想,但他在当时并没有提出“形而上学”这个概念,后来在亚里士多德哲学中,这个概念才被正式提出来。
亚里士多德是一位百科全书式的人物,也是希腊哲学的集大成者。亚里士多德有个特点,就是述而不作。他提出了很多观点、理论,但他生前真正表述自己思想的书籍却很少,大部分有关亚里士多德思想的著作都是由他的弟子记载并整理而成的。

亚里士多德
亚里士多德曾在雅典一个名叫吕克昂的体育场创立了自己的学院——吕克昂学院,专门收徒授课,所以他的哲学学派也被称为吕克昂学派。
吕克昂学派还有个名字,叫作逍遥学派,原因是学院里面有很多长廊,而亚里士多德喜欢一边带着学生在长廊中散步,一边给学生授课,同时还会与学生讨论各种哲学问题。亚里士多德从来不会让学生在课堂中正襟危坐地听他讲课,他教授给学生的内容也仅靠学生随手记录。

逍遥学派
亚里士多德死后,他的学生和后人们开始分门别类地整理他的思想及观点,并将其汇编成不同的著作。比如,亚里士多德研究自然科学时产生的思想被编成一本书,书名为《物理学》,他研究逻辑学时产生的思想也被整理成一本书,书名为《工具篇》。
此外,还有研究政治学思想的《政治学》、研究文学艺术思想的《诗学》以及研究伦理学思想的《尼各马可伦理学》(由亚里士多德的儿子尼各马可编纂成书),等等。

当亚里士多德的传人们把他所有的思想整理成书后,他们发现有一部分内容是亚里士多德最为重要的思想内容,他本人将其称为“第一哲学”,也就是“最重要的哲学内容”,但这部分哲学内容既不属于物理学、逻辑学,又不属于政治学、伦理学、诗学,因为这些学问研究的对象都是具体存在的事物。
比如研究作为自然现象的存在、作为社会现象的存在、作为文艺现象的存在,等等,但是“第一哲学”是研究“存在”本身的哲学。简而言之,我们在研究某事物为什么存在之前,首先要研究存在本身。

比如,想要研究男人、女人、坏人、好人,那么首先要研究人,知道人是什么,然后才能区分并研究男人、女人、坏人、好人。同样,在研究作为自然现象的存在、作为社会现象的存在或作为文艺现象的存在之前,首先要研究存在本身。
而亚里士多德研究存在本身的学问就是第一哲学,也是亚里士多德最重视的哲学内容。因此,这部分内容无法被归纳到物理学、逻辑学、伦理学等具体的学问当中,但又不能直接将其称为第一哲学。
于是,亚里士多德著作的整理者们就采取了一个权宜之计,他们将这部分内容单独编成一卷,放在《物理学》这卷的后面,还为这部分内容起了一个体现其权宜之计特点的名字——“在物理学之后”,即“metaphysics”。

随着哲学的不断发展,亚里士多德作品中的其他著作,如《物理学》《政治学》《诗学》等,逐渐从哲学中分离出来,唯独最重要的那部分——“metaphysics”发展为真正意义上的哲学,成为亚里士多德的哲学内容中最为核心的部分。
到了19世纪,日本人接受了西方思想文化之后,开始用中国文化中的一些术语去翻译西方的著作,“形而上学”一词最早就是由日本明治时期著名哲学家井上哲次郎翻译出来的。《易经·系辞》中有这样一句话:“形而上者谓之道,形而下者谓之器。”意思是说,有形的、看得见、摸得着的东西,称为器;而无形的、超越性的东西,称为道。

日本明治时期著名哲学家井上哲次郎
由于器用之物有形,所以称其为形而下;而道是无形的、抽象的,所以称其为形而上。井上哲次郎在翻译“metaphysics”这个词时参照了这句话,将亚里士多德的“第一哲学”翻译为“形而上学”。这一翻译极其精到,顾名思义,亚里士多德的“第一哲学”是研究“道”的学问,是形而上的、极其高深的哲学思想。
“形而上学”的西文概念产生后,一直到中世纪乃至西方近代早期,它都是一个褒义词,指代一种非常高深的学问,是哲学的本质和核心所在。但到了康德那里,康德开始批判“形而上学”,他认为“形而上学”太过玄奥,虚无缥缈,人们在理解时容易产生主观谬误。

康德
再到后来的黑格尔那里,“形而上学”就变成了一个贬义词,黑格尔在批判“形而上学”时,还提出一个与“形而上学”相对立的理论——辩证法。
很多人认为“形而上学”是一个贬义词,把它理解为一种片面地、孤立地、一成不变地看问题的思维方式或哲学体系。但这并不妨碍西方思想家和哲学家们将“形而上学”当成是哲学思想中最为重要、最为核心的部分,是哲学的灵魂。

弄清了“形而上学”的概念,再回到毕达哥拉斯学派,我们就会发现,毕达哥拉斯学派其实开创了一条注重事物背后的抽象实质的形而上学路径,这是一条与希腊自然哲学完全不同的路径,并且它更具哲学味道。
古希腊哲学的基本目标就是寻求万物的本原,在这个基本目标的指引下,自然哲学侧重于说明一与多的关系,而形而上学则更加注重探讨本质与现象的关系。希腊自然哲学后来在德谟克利特的“原子论”中最终实现了一与多的统一,而希腊形而上学在其开端处就明确地将“一”本身作为万物的本原。

德谟克利特的“原子论”
这里的“一”指的不是某种具体的物质形态,而是抽象的数,或者说是一种不生不灭、不变不动、始终如一的本质。从这个意义上来说,它其实就是万事万物必须遵循的命运或逻各斯。这样一来,“一”就从毕达哥拉斯的形而上学意义上的数,自然而然地过渡到了赫拉克利特的更加抽象的分寸、尺度或逻各斯。
四、数与形的分离与赫拉克利特的二元论毕达哥拉斯在数学上取得了一个伟大成就,就是发现了勾股弦定理。但这个定理的发现很快引起了数学史上一场大危机,即不可通约数危机。
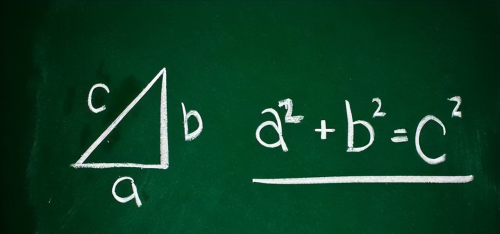
勾股弦定理
在毕达哥拉斯学派中,有一个名叫希伯索斯的人,他也是一位精通数学的哲学家。他发现,如果一个直角三角形的两条边都为1,那么根据勾股弦定理,它的斜边是多少呢?
今天我们自然知道,斜边是√ ̄2 。√ ̄2 既不是奇数,也不是偶数,而是一个无理数。但在当时的希腊,人们只知道两种数:奇数和偶数,对无理数一无所知。在希腊人看来,如果不能用一个整数表示这条斜边,那么至少可以用分数表示。
根据毕达哥拉斯定律,这个分数的平方等于2,因此这个分数的值应该大于1且小于2。于是人们开始通过归纳的方法寻找这个分数,可是不论如何推理,都找不到这样一个其平方为2的分数。

如此一来,希腊人便迷惑不解了,连毕达哥拉斯自己也开始困惑:明明可以画出这样一个直角三角形,三角形也有一条斜边,为什么找不到表示这条斜边的数呢?也就是说,这条斜边与另外两条直角边是不可通约的。这种状况让希腊人对数与形之间的对应性产生了怀疑,也让数变得更加神秘化。
据说希伯索斯因为动摇了毕达哥拉斯定律追求的逻辑完美性,让毕达哥拉斯学派陷入困惑和尴尬之中,他被驱逐出毕达哥拉斯学派,后来被人推到大海里淹死了。但不可通约数危机撕裂了毕达哥拉斯学派在数与形之间建立的同一性,导致了二者的分离,从而产生一种将数神秘化的倾向。

希伯索斯
形是形而下的,数却是形而上的,明明可以画出形来,却找不到对应的数,如此令人尴尬的结果不仅使数变得神秘莫测,还导致了一种把抽象的数看得比具象的形更加真实、更加具有本质性的认识倾向,从而奠定了西方哲学史中重理性、轻感性的唯理论传统。
或许正是受到了毕达哥拉斯学派关于数与形相互分离的思想的影响,后来的赫拉克利特认为哲学具有复线关系:一方面,赫拉克利特认为世界是火与万物在周而复始地不断转化;另一方面,他又强调火与万物之间的转化会受到逻各斯的制约。

赫拉克利特
这样一来,变动不居、杂而多的自然万物与不变不动、单一的逻各斯之间形成了两条平行线索。显然,赫拉克利特将逻各斯当成了万事万物背后那个不出场却起着决定作用的“导演”,这是由于他深受毕达哥拉斯“数本原说”的影响,把万物的抽象本质进一步由数深化为质(逻各斯)。
毕达哥拉斯学派自恃精通数学,将不懂数学的芸芸众生拒之于神圣的哲学殿堂之外。赫拉克利特则认为,逻各斯对所有人都是一样的,只是绝大多数人对逻各斯视而不见、充耳不闻。

赫拉克利特
他的言外之意就是,普罗大众的思想充其量只能停留在火与万物的转化这个表象上,看不到表象背后的逻各斯,而他却可以看到逻各斯。所以他不屑与大众为伍,离群索居,孤芳自赏,用他自己的话来说,“一个最优秀的人抵得上一万个人”。
毕达哥拉斯和赫拉克利特这种关于数与形、逻各斯与具体事物的二元对立思想,表现出了强烈的精英主义色彩。其实,希腊后来许多哲学家都有这种观念,认为只有自己才能把握真理,而芸芸众生只能沉溺于意见之中。

毕达哥拉斯
早在毕达哥拉斯那里就明确地划分出一对相互对立的概念,即真理与意见,其中真理指的是智慧,意见则是指常识、俗见。这也让希腊哲学,尤其是形而上学走上了一条与大众见识背道而驰的道路。
赫拉克利特还提出,火与万物是多,逻各斯是一 ;火与万物是动,逻各斯是静;火与万物是有生有灭,逻各斯是不生不灭。只有关于独一无二、不动不灭的东西(逻各斯)的知识,才是真正的智慧,后来这种观点也贯穿了整个希腊的形而上学。
这样一种彼此独立又互相平行的复线观点,便构成了赫拉克利特的“二元论”。但是,赫拉克利特并没有因为逻各斯理论而放弃火本原说。在赫拉克利特那里,逻各斯与火及万物构成了一种复线关系,它们都是真实的,只是相比而言,逻各斯更具真理性,对逻各斯的认识才是真正的智慧。
温馨提示:通过以上关于浅析希腊哲学之——毕达哥拉斯学派2内容介绍后,相信大家有新的了解,更希望可以对你有所帮助。