鸟头模型数学题(小学鸟头模型公式推导过程)

小学数学竞赛必备——五大模型之鸟头模型

鸟头模型，是平面图形中常用的五个模型之一，其特点是通过边与面积的关系来解决问题。对于初学者来说，最重要的是理解什么是鸟头模型并熟记它的特征。

一、鸟头模型的相关知识

1.定义：两个三角形中有一个角相等或互补（相加等于180度），这两个三角形就叫共角三角形。这个模型就叫鸟头模型。其中存在的比例关系就叫做共角定理。

2.核心：比例模型有：

二、鸟头模型的原理剖析

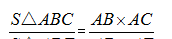
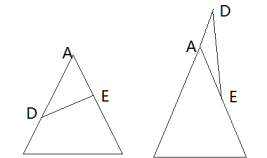
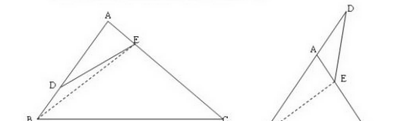
证明：在三角形ABC中，连接BE，

则有：

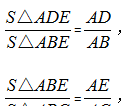
利用等式的性质，左右两边分别相乘得：

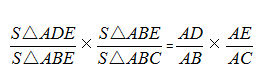
即：

三、鸟头模型的方法运用

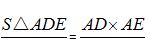
鸟头模型解题四部曲：

第一步：观察：图中是否有鸟头模型

第二步：构造：鸟头模型

第三步：假设：线段长度或图形面积

第四步：转化：将假设的未知数转化到鸟头模型中计算

【例1】如图，在三角形ABC中，D、E是AB,AC上得点，且AD：AB=2:5，AE：AC=4：7，三角形ADE的面积是16平方厘米，求ABC的面积。

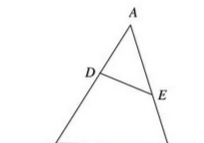
解析：

①观察：图中存在鸟头模型

②假设：设三角形ABC的面积为a

③ƒ转化：由鸟头模型比例关系有：16：a=（4×2）：（5×7），得a=70,。即三角形ABC的面积是70平方厘米。

【例2】如图，四边形EFGH的面积是66平方厘米，EA=AB,CB=BF,DC=CG,HD=DA,求四边形ABCD的面积。

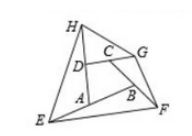
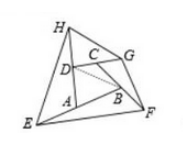
解析：

①观察：图中不存在鸟头模型。

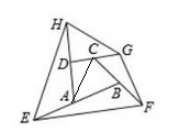
②构造：如图2，连接BD，则三角形BDC和三角形CGF以及三角形ABD和三角形AHE构成鸟头模型。如图3，连接AC，则三角形ADC和三角形DGH以及三角形ABC和三角形BEF构成鸟头模型。

③转化：

在图2中，由共角定理得：S△BCD：S△CHF=（CD×CB）:（CG×CF）=（1×1）：（1×2）=1:2。

同理可得：S△ABD：S△AEH=1:2。

在图3中，同理S△ ADC：S△DGH=1:2，S△ABC：S△BEF=1:2。

S△BEF=2S△ABC，S△AEH=2S△ABD，S△DGH=2S△ADC。S△CFG=2S△BCD ，所以S四边形EFGH==5S四边形ABCD。 S四边形ABCD=66÷5=13.2平方厘米。

温馨提示：通过以上关于小学数学竞赛必备——五大模型之鸟头模型内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。