计量型控制图有哪些(计量型控制图和计数型控制图的区别)

一文读透计量型控制图建立与分析

今天有个小伙伴又来了一个新的问题。

问题是这样的：“我今天把我们一个量产的产品重要尺寸根据统计数据做了SPC报告提交给领导去审核，计算得出CPK的值为1.47，按照要求已经大于了1.33，领导确说这个值没有参考意义，这是为啥呀！？”我看了一下他的报告控制图表，原来控制图表有一个异常点存在，他并没有剔除分析原因，自然计算的得出的CPK值就失去了意义。今天我们就来说一下控制图的制作与分析。

在讲解控制图之前，我们先来回顾一下上篇文章提到的CP和CPK的使用前提，然后我们再来细说控制图的制作及分析过程：

“CPK的计算必须满足过程稳定和数据正态分布两个必要条件，没有这两个必要条件所计算出来的Cp和Cpk值是不具有统计学意义的，或者说所得到的Cp和Cpk 不准确。”

那么建立控制图的分为5个步骤：

1、控制图准备

2、收集数据

3、建立控制限

4、过程控制解读

5、延长控制限

下面我们对每一个步骤如何进行来详细解读一下：

1、控制图准备

我认为准备工作，比做一件事更重要，如果你准备的很充分的话，那么我们做就会很容易。

那么我们该怎么准备呢？

首先，要建立过程环境，也就是说要想做这个控制图，首先要给条件。

第二，要定义过程，即我到底研究哪一个过程特性。所以，确定控制图的研究对象的特性是什么，那么这个特性，建议大家要选择顾客所关心的特性。

第三，要确认到底要解决什么问题？选择当前或潜在的问题区域的特性进行研究。如果一个特性控制图已经很好了，这个过程已经控制的非常稳定，就没必要检验它，研究它，因为已经很稳定了。我们解决问题，总要找最关键的，客户（往往不紧指购买产品的客户，也包含我们内部其他部门或者领导）最为关心的问题。

第四，要研究特性之间的关联性，有的特性不好研究或者说研究它花的代价很高，那么这时候怎么办呢？需要找到相关联的特性，是否满足要求，比如说汽车上的压力罐，测试的极限耐压程度，它是一个破坏性的实验，你把它测试完了，它是合格了，但是产品也废了。大家都知道，极限耐压主要还是关注它的焊接是否达到了这个要求，这时候可以通过控制它的焊接电流，焊接电压。通过控制焊接的一种参数来保证最终的结果（这个例子仅作为举例说明助大家理解）。所以有些是需要找到特性之间的关联性的，只有这样研究才会更加有意义也方便。

2、收集数据。

我们第一个步骤准备好了，我们找到了研究对象，那么下面怎么办？开始收集数据。那怎么来收集数据好？

收集数据的时候，我们要抓住两点：

首先，要确定收集多少个数据（子组容量）。要求最少要有25个子组，建议最好收集30组；

其次，要确定多长时间收集一组数据和一组收集几个数据。确定子组与子组之间的间隔时间，一个子组收集几个数据，那么还需要考虑第一个子组跟第二个组间隔多长时间收集，还有这一个子组收集五个数据，这五个数据什么时间收集。

这里重点强调一个取样原则：“组内变异小，组间变异大”原则。也就是说抽样方法就是这两句话，组间变异大，就是说子组与子组之间变化的时间要间隔长一点；组内变异小，就是说一个子组内的几个数据要连续抽样，这样变异就会少。

举个例子：每间隔两天收集一组数据（组间变异大），一组开班后连续收集前五个产品数据（组内变异小），直到收集够25组数据。

只要把这几个问题解决了，那么我们的数据收集也就没有问题了。

3、建立控制限和控制图

首先要计算每个值组的平均值或每个值组的极差，接着描点制作控制图，最后就是建立控制界限。这个我们就不展开描述了，现在利用minitab软件或者自己编制的Excel模板都可以实现，不需要我们手动计算和画图。

4、过程控制解读

我们之所以要用控制图的目的，就是要及时发现过程中出现的异常，这里所指的异常在统计学理论中就是“小概率事件”。

我们这里先列一些SPC手册里面的8个典型特殊原因识别准则，这8个识别准则可以总结为两类：

第一类：准则1作为首先判定原则。因为1个点超过控制限的概率为0.27%，为小概率事件。

第二类：准则2-8根据统计学原理算下来也属于小概率事件，在排列形状上就可以判定其有缺陷。

大家注意到计量型控制图控制总共有2个控制图Xbar图和R图，首先来分析R控制图，然后再分析Xbar图，这两个控制图不能违反上述的8条准则。为什么要这样呢？因为在统计分析过程中，均值被用于位置的控制统计量，极差用于变差的控制统计量。而位置的统计量的控制限依赖于变差的统计量的变化，变差的控制统计量首先被分析以检查稳定性。除非两个图都没有不受控的情形（显示特殊原因），否则一个过程是不能够成为稳定的（统计受控）。

休哈特的这8条准则记忆的时候可能比较困难，很容易忘记，那我再给大家介绍一下比较实用的判定原则：“点线面”原则。

这里多啰嗦一下，我们看一张控制图形的时候不是看它的图形变化的一种曲线，有规律还没有规律，我们反而看它是没有规律的。越是没有规律的控制图反而越是好控制图，这说明是符合随机性原则。

废话不多说了，现在开始说一下“点线面”原则。

“点”原则（休哈特准则1）：看这个控制图上面有没有点子超过控制界限，如果有一点或者说多个点子超过任何一条控制界限，那么认为这个控制图异常。为什么这样说？因为休哈特控制图的工作原理就是只控制99.73%，剩下还有0.27%没有控制。那么一个点子出现在控制线之外的概率是多少？因为控制图是对称的，所以出现的概率是0.135%。这是一个非常小概率事件，也就是说在这25个点事件下，发生的机会只有0.135%，我们认为是不可能发生的事件。最终认为它是异常的。

“线”原则（休哈特准则2-3）。如果在一个控制图中间，有连续7点在中心线的同一侧，连续7点上升或下降，那么我们认为这个控制图，都是异常的。我们简单分析一下连续7点在中心的同一侧也判定为异常的。一个点落在中心线一侧控制限范围内的概率为99.73%/2=49.865%，那么那么这七个点都落在中心线一侧控制限范围内的概率为（49.865%）^7=0.77%。那么发生这种机会是概率非常小的，所以判定它就是异常的，这是我们控制图的一个原理。另外两种情形这里就不展开说了，计算方法一致。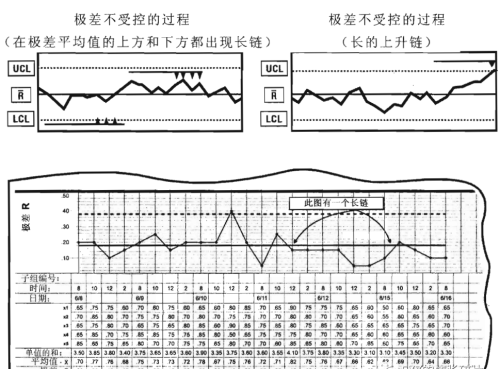

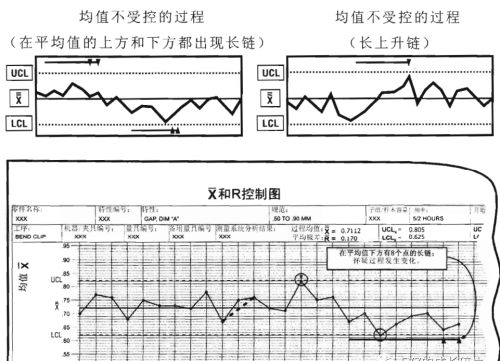“面”原则。明显的非随机图形，应依正态分布来判断图形，正常应是有2/3点落在中间1/3的区域（±1σ的区域面积）。按照我们正态分布的趋中心的一个特点，在±1σ的范围内，它的面积是68.27%。统计讲的是大概，那么68.27%大概为2/3。所以应该有多少2/3个点子应该集中在什么中间的1/3区域，如果是这种现象，说明它是正常的，反之它就是异常的。也就是说，如果有25个点子的话，大概应该要有16个点到17个点子，集中在这个控制图的中间的1/3区域，其余的八个点子或者说九个点子分布在两侧，这就是“面”判定准则。这个不太好理解，大家不用纠结，主要记住这个结论就好！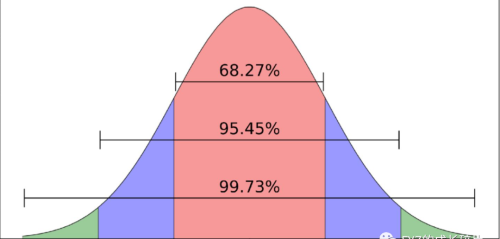

5、延长控制限

如果这控制图是好的，就延长控制线。这个很简单，就不多解释了。

最后再说明一点：

当第四步分析的时候控制图违反了“点线面”判定原则情况，首先把这个点子给去掉，然后重新收集数据，再重新计算控制限，一直计算到没有发生的时候为止，那么控制图才算合格的。这也是为什么建议大家在做计量型控制图的时候，一开始要多收集数据，大概30个子组的原因。就是防止收集30个子组中间，若发现有一两点出现异常的，就可以把这个异常点子给去掉，重新来计算控制。

在实际使用分析控制图的时候建议先考虑“点线面”这三条准则。休哈特其他的判定准则其实是用来做参考的，不能做你的判定的所有的依据，否则肯会加大一种虚发警报的可能性，所以实际的控制图判定稳定不稳定，“点线面”判定准则就够用了。

温馨提示：通过以上关于一文读透计量型控制图建立与分析内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。