质数,合数,公约数,公倍数(质数合数公倍数公因数的概念)

省考招警行测备考指导：质合数与公约数公倍数的故事

质数与合数在实际求解过程中，不止可以求解经典题型：(1)求一个数的正约数的个数;(2)约数的分组问题。在行测考试中，还有这样一类题目，需要求解若干个数的公约数和公倍数。

首先，让我们先来了解一下约数和倍数：一个自然数A能被自然数B整除且B不为0，我们就称A是B的倍数，B是A的约数。

那么，什么是公约数和公倍数呢?一个数M同时是若干个数的约数，则M就是这几个数的公约数;一个数N同时是若干个数的倍数，则N就是这几个数的公倍数。

根据约数B最大不会超过A，可知，公约数M在有限条件内有最大值，称为最大公约数;同时，倍数A最小不小于B，则公倍数N有满足条件的最小值，成为最小公倍数。

其次，如何求解最大公约数和最小公倍数，方法：短除法。如下图：

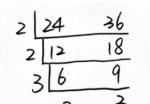
最大公约数=2×2×3=12;最小公倍数=2×2×3×2×3=72。

【总结】

求解原则：最大公约数为几个数共有的约数的乘积;最小公倍数为几个数共有的约数与自身剩余的质数的乘积，若为三个数及以上，则需保证自身剩余的质数两两互质(即除1以外再无共同的约数)。

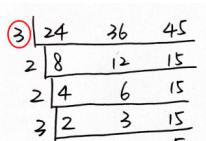
最大公约数=3(三者共有的约数);最小公倍数=3×2×2×3×2×1×5=360(2、1、5任意两个数均为互质)。

对于公约数和公倍数的考查，有些题目能够直观的判断出来，而有些却不容易。

例1、一张长方形纸，长2703厘米，宽1113厘米，要把它截成若干个同样大小的正方形，纸张不能有剩余且正方形的边长要尽可能大。问：这样的正方形的边长是多少厘米?

A.153 B.156 C.158 D.159

【思路点拨】

根据题目要用长方形彩纸裁剪正方形，并要求纸张不能有剩余且正方形的边长要尽可能大，据此可知，边长是长方形长和宽的公约数且为最大公约数。

方法一：直接根据选项带入排除，由于尽可能大，则从选项D开始带入，符合题干条件，D正确。

方法二：根据长和宽的奇偶性(为奇数)可知，边长×裁剪个数为奇数，则边长和个数均为奇数，则排除B、C，同上分析带入D正确。

例2、甲每4天逛一次超市，乙每7天逛一次，丙每10天逛一次，某天3人在此超市相遇，那么三人下次相遇至少需要经过多少天?

A.28 B.40 C.70 D.140

【思路点拨】

要求三人下次相遇至少需要经过多少天，可知要想三人相遇，经过的天数必须是4、7、10的公倍数(甲每4天去一次，则8天去两次，依次类推，可知甲去超市经过的天数为4的倍数，同理得到乙、丙的结论，又因为三者同时去，则应为三者的公倍数)，则要求经过的最少天数即为最小公倍数为140，则D正确。

【总结】

1、 公约数、公倍数题目首先须根据题干条件分析所求解数据与已知数据之间满足相应的整除条件(或约数与倍数的关系)。

2、 根据题干关系，判断求解数据或计算中需要的数值为最大公约数还是最小公倍数。

3、 确定题目所求答案。

温馨提示：通过以上关于省考招警行测备考指导：质合数与公约数公倍数的故事内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。