导数为什么是切线斜率(为什么导数是切线)

导数为什么就精确等于切线斜率

我们知道，对于匀速运动来说，速度等于一段时间内移动的距离与这段时间的大小之比。

但对于变速运动来说，速度怎么求呢？

这里的问题在于，理想的变速运动，是在每一个点上速度都是变化的，而数学上的点是没有大小的。那怎样才能求出变速运动中每个没有大小的点上的速度呢？

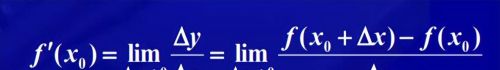
导数的定义如上图。这里的关键在于，delta x是趋于0的。那这里的无限趋于0该怎么理解呢？我们看下图：

现在假设我们要求的是中间那个点的速度，那么我们可以这样认为：当时间t在无限趋近于中间那个时间点t0的时候，已经进入了上图的delta区域，在这个区域内，其它时间点与t0这个时间点之间的差距delta已经无法用任何一个数字来表示，我们也就可以认为，这个区域内只有t0这一个点。这就保证了导数定义中求变速运动中某个固定点速度的问题。

我们知道，导数就等于曲线在这个点上的切线的斜率。注意，不是约等于。

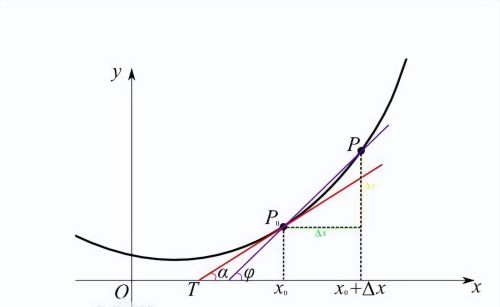
如上图。在割线P0P无限趋近于P0那条切线的过程中，似乎总会存在那么一点差距，但当割线和切线完全重合的时候，似乎切线和曲线又只有一个交点。那怎么理解导数就是切线的斜率这个事实呢？

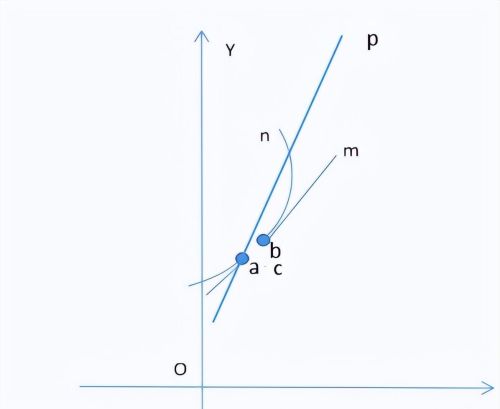
上图表明，割线在向切线无限趋近的过程中，一定能够找到除了切点a之外的另外一个点b，点b同时在切线和曲线上，理论依据就是数学上的点是没有大小的，我们甚至可以进一步认为，除了点b之外，再没有第三个点同时在曲线和切线上面，点b也是最靠近点a的那个点。既然点没有大小，当我们想找到上图的b点的时候，我们就可以采取想怎么接近就怎么接近的方法找到它。找到b点之后，我们就可以用a,b,c三点构成一个直角三角形，从而在这一点上，曲线的斜率就等于切线的斜率，两者之间不存在任何误差。

简单来说：

1：导数是用来求数学上某个点的变化率的，而且这个点在数学上是没有大小的。

2：导数表示曲线上某一点的变化率就等于这一点切线的斜率，而不是约等于。

温馨提示：通过以上关于导数为什么就精确等于切线斜率内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。