求旋转面表面积(旋转图形表面积公式高等数学)

标题：旋转表面积公式的魔力

现在越来越少教的公式

上面的公式给出了通过围绕x轴旋转曲线y = f(x)形成的形状的表面积（不包括该形状两端的表面，如果有的话）。它过去在高中课程中很常见，但我发现它现在在学校中出现的次数越来越少。我想用这篇文章来说明这个公式的一些有趣和有用的应用。

球体切片的表面积

通过围绕 x 轴旋转等式x² + y² = r²的圆形成球体，其中r是圆的半径。现在想象一下，我们想要找到通过在两个平行平面之间切片而形成的球体表面积的一部分。

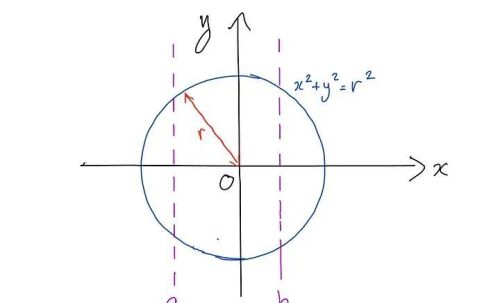
这相当于在曲线x² + y² = r²上使用我们的公式，按照上图在两个任意值a和b之间积分。

现在微分我们的圆方程关于x，我们得到

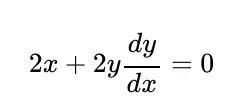
这给了我们

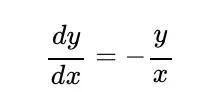
将其放入本文顶部的公式中，我们有

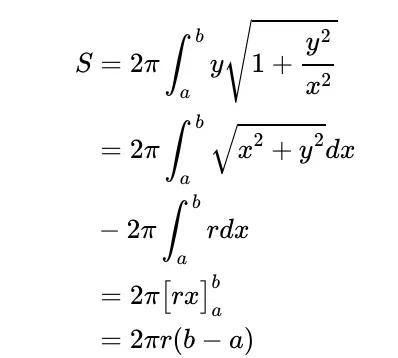
所以这部分表面积是 2π r乘以切割它的平面之间的垂直距离。多好！当然，如果我们将垂直距离作为球体的直径，我们得到球体的总表面积为 4π r²，这证实了标准公式。

计算“冰淇淋甜筒”的表面积

取一个一定半径的圆，从原点到圆上的某一点 P 作切线，然后绕x轴旋转，就可以形成一个“冰淇淋锥” 。这张照片应该有所帮助。我们说圆的半径为a ，圆心为(c, 0)，c > a，我们从原点 O 绘制点 P 的切线：

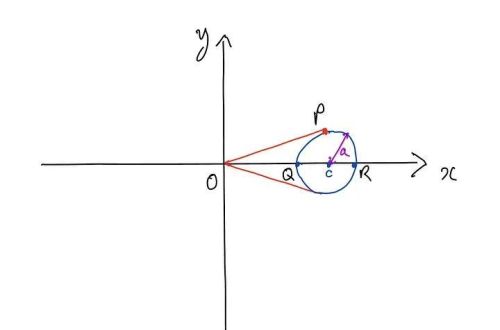
为了获得冰淇淋蛋筒的形状，我们采用直线OP和曲线段PR并围绕x轴旋转它们。因此，我们可以通过对这些部分中的每一个使用我们的神奇公式来获得冰淇淋甜筒的表面积。为此，我们需要找到点P的x坐标。

如果我们在 P 处画一条垂直于切线的法线，我们知道法线穿过圆心，因此如果长度为a则它是一个半径。这形成了一个直角三角形，顶点为O、P和圆心。因此，使用毕达哥拉斯定理，我们说OP的长度为 √( c² — a²)。因此，我们可以计算梯度，从而计算我们的线OP 的方程：

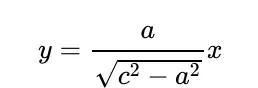
和

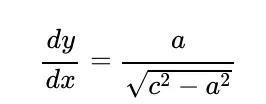
现在点P是 OP 和我们的圆的交点，它有等式：

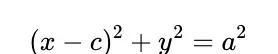
求解圆和线OP的联立方程，我们可以找到P的x坐标，结果是（c²-a²）/c。

因此，使用我们的神奇公式，我们可以计算出冰淇淋锥体部分的表面积：

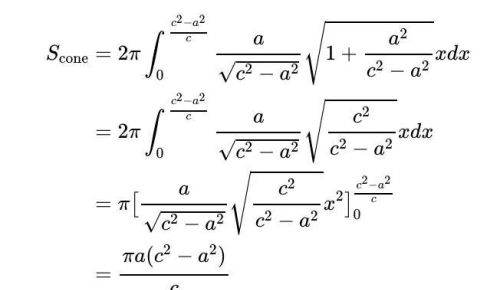
现在要找到冰淇淋蛋筒的“冰淇淋”部分的表面积，即PR 段的旋转，我们注意到这是 ( c² — a²)/c和c之间的球体切片+ a，所以使用上一节的结果，这是：

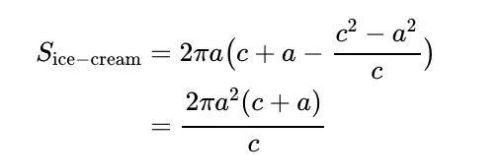
所以我们的冰淇淋甜筒的总表面积是：

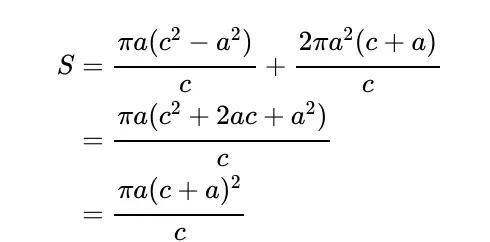
温馨提示：通过以上关于标题：旋转表面积公式的魔力内容介绍后，相信大家有新的了解，更希望可以对你有所帮助。