随机过程的平稳与遍历的关系(随机过程的平稳与遍历的区别)

导语：随机过程的平稳与遍历

随机过程，是依赖于参数的一组随机变量的全体，参数通常是时间。随机变量是随机现象的数量表现，其取值随着偶然因素的影响而改变。例如，某商店在从时间t0到时间tK这段时间内接待顾客的人数，就是依赖于时间t的一组随机变量，即随机过程。

随机过程的理论产生于本世纪初期，是应物理学、生物学、管理科学等方面的需要而逐步发展起来的。目前，在自动控制、公用事业、管理科学等方面都有广泛的应用。

随机过程有一些重要特征，比如，平稳、遍历等。先看平稳性。

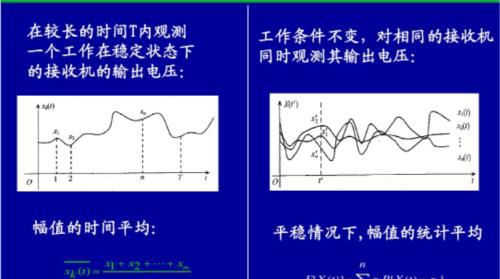
图一

图二

从图一和图二的解释中，我们可以看到，所谓的随机过程，就是很多个随机变量放在一起，如果把随机变量看成一条曲线，那么随机过程就可以理解成由很多条曲线组成的平面。为了更好地理解这个概念，以下面这个图中掷骰子的过程为例。

图三

图三中的一行，表示一个骰子掷了很多次；图三中的一列，表示一个时刻掷了很多个骰子。理想的随机过程，就是图3中的 行列都无穷大。我们知道，掷骰子的均值=1x1/6+2x1/6+3x1/6+4x1/6+5x1/6+6x1/6=3.5,图一图二中所表示的平稳的含义，其实就是表示图三中的每一行和每一列的均值都等于3.5；各态历经指的是图三中的任何一行和任何一列都只可能出现

1，2，3，4，5，6这六个数字，而且这六个数字在每一行和每一列中出现的概率都是1/6。

再看什么是相关各态历经：

图四

图四表明，相关各态历经的意思就相当于图三中任取两列，然后把这两列每一行上两个骰子的数值相乘然后相加所得的结果，和取的是哪一列无关，只和这两列的间隔有关，比如：第3，7列与第4，8列的相关结果相同，因为他们的间隔都是4，但与第3，5列的结果不同，因为两者的间隔是2。相关各态历经表示的意思是指：在图三中任取两列，虽然图三中每一列出现六个数字的可能性都是1/6，但这六个数字在这一列的哪一行上出现，这种可能性的不同仅仅和这两列的间隔有关，而和具体是哪两列无关。

最后看一个例子。

结果表明例子中的随机过程具有自相关遍历性。

本文内容由小芦整理编辑！