中考试题中的动点问题有哪些(中考试题中的动点问题是什么)

导语：中考试题中的动点问题

26.（本题满分8分）

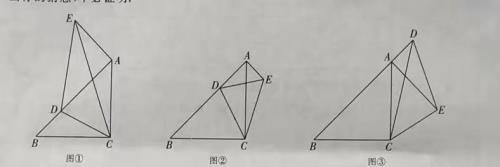
在△ ABC 中， AC = BC ,∠ACB =90°, D 是射线 BA 上一动点，连接 CD ，以 CD 为边作∠DCE =45°, CE 在 CD 右侧， CE 与过点 A 且垂直于 AB 的直线交于点 E ，连接 DE .

当 CD 、CE 都在 AC 的左侧时，如图①，线段 BD , AE , DE 之间的数量关系是

(2）当 CD 、 CE 在 AC 的两侧时，如图②，线段 BD , AE , DE 之间有怎样的数量关系？写出你的猜想，并给予证明；

(3）当 CD 、 CE 都在 AC 的右侧时，如图③，线段 BD , AE , DE 之间有怎样的数量关系？直接写出你的猜想，不必证明．

解：（1）三者之间的关系是：DE=BD+AE

证明：延长EA到点F，使AF=BD，连接CF

∵CA=CB,∠ACB =90°

∴∠B=∠BAC=45°

又∵AF=BD

∴△ BDC ≌ △ FAC

∴CD=CF，∠BCD=∠FCA

∵∠ACB =90°,∠DCE =45°

∴∠BCD+∠ACE=45°

∴∠FCA+∠ACE=45°=∠FCE

在△ CDE和 △ CFE 中，

CD=CF，∠DCE=∠FCE=45°，CE=CE

∴△ CDE ≌ △ CFE

∴DE=EF

∴DE=EF=AE+AF=AE+BD

解：（2）三者之间的关系是：BD=DE+AE

证明：延长EA到点F，连接CF，使∠DCF=90°。

∵∠BCD+∠ACD =90°,∠ACF+∠ACD =90°

∴∠BCD=∠FCA

∵CA=CB,∠ACB =90°

∴∠B=∠BAC=45°

∵EA⊥AB

∴∠EAB =90°

∴∠FAC=∠EAB-∠BAC==∠B

∴△ BCD≌ △ ACF

∴BD=AF，CD=CF

∵∠DCF=90°,∠DCE =45°

∴∠ECF=∠DCE=45°

∵CE=CE

∴△ CDE≌ △ CFE

∴DE=EF

∴BD=AF=AE+EF=AE+DE

解：（3）三者之间的关系是：BD=DE+AE

证明：在线段BD上取一点F,使BF=AE，连接CF。

∵CA=CB,∠ACB =90°

∴∠B=∠BAC=45°

∵EA⊥AB

∴∠EAB =90°

∴∠EAC=∠EAB-∠BAC==∠B

∵CA=CB,AE=BF

∴△ AEC≌ △ BFC

∴CF=CE，∠ACE=∠BCF

∵∠BCF+∠ACF =90°

∴∠ACE+ACF =90°

∵∠DCE=45°

∴∠FCD=∠DCE=45°

∴△ FCD≌ △ ECD

∴DF=DE

∴BD=BF+DF=AE+DE

本文内容由快快网络小洁整理编辑！