电磁感应中的电路电荷量问题(电磁感应中的电路问题)

导语：电磁感应中的电路

1、电磁感应中的两类电路问题

（1）以部分电路欧姆定律为中心，包括六个基本物理量（电压、电流、电阻、电功、电功率、电热），三条定律（部分电路欧姆定律、电阻定律和焦耳定律）以及若干基本规律（串、并联电路特点等）.

（2）以闭合电路欧姆定律为中心，讨论电动势的概念、闭合电路中的电流、路端电压以及闭合电路中能量的转化.

2.解决电磁感应中的电路问题的“三部曲”

（1）确定电源

切割磁感线的导体或磁通量发生变化的回路产生感应电动势，该导体或回路就相当于电源，利用E＝n△φ/△t或

E＝Blv求感应电动势的大小，利用右手定则或楞次定律判定电流方向、如果在一个电路中切割磁感线的有几个部分但又相互联系，可视为等效电源的串、并联.

（2）识别电路结构、画出等效电路

分析电路结构，即分清等效电源和外电路及外电路的串并联关系、判断等效电源的正负极或电势的高低等.

（3）利用电路规律求解

一般是综合应用欧姆定律、串并联电路特点、电容器充电及放电特点、电功和电功率的知识、法拉第电磁感应定律等列方程求解.

3.与电学问题相关的规律

（1）电源电动势：E＝n△φ/△t或E＝Blv.

（2）①闭合电路欧姆定律：I=E/R＋r.

②部分电路欧姆定律：I＝U/R

③电源的内电压：U内＝Ir

④电源的路端电压：U外＝IR＝E-lr

（3）消耗功率：P外＝IU，P总＝IE，P热＝I²r或P热＝I²R

（4）通过导体的电荷量：q＝I△t＝n△/φ/(R＋r)

（5）电路中的焦耳热：Q＝I²（R＋r）t或Q＝△E

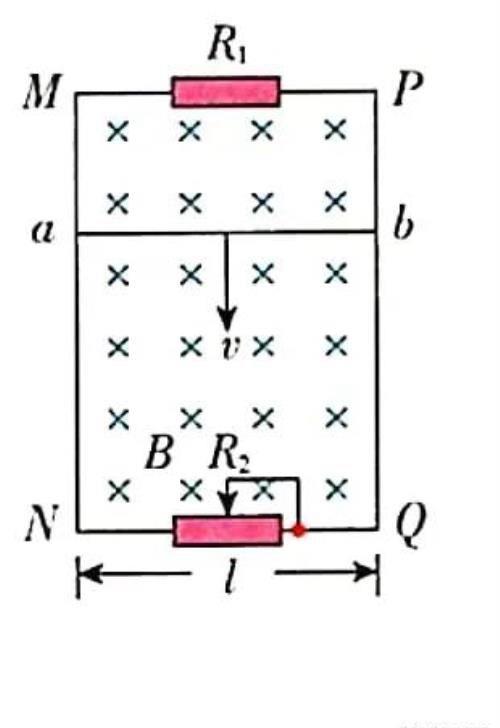
例：如图所示，

MN和PQ为竖直方向的两平行长直金属导轨，间距l＝0.40m，电阻不计.导轨所在平面与磁感应强度B＝0.50T的匀强磁场垂直.质量m＝6.0×10⁻³kg、电阻r＝1.0Ω的金属杆ab始终垂直于导轨，并与其保持光滑接触.导轨两端分别接有滑动变阻器和阻值为3.0Ω的电阻R₁.当杆ab达到稳定状态时以速率v匀速下滑，整个电路消耗的电功率P为0.27W，重力加速度g取10m/s²，求：

（1）杆ab达到稳定状态时的速率v；

（2）滑动变阻器接入电路部分的阻值R₂.

【方法总结】（1）“电源”的确定方法：切割磁感线的导体（或磁通量发生变化的闭合线圈）相当于“电源”，该部分导体（或线圈）的电阻相当于电源的“内阻”.

（2）电流的流向：在“电源”内部电流从负极流向正极，在“电源”外部电流从正极流向负极.

例：如图所示，

由均匀导线制成的半径为R的圆环，以速度v匀速进入一磁感应强度大小为B的有直线边界（图中竖直虚线）的匀强磁场中.当圆环运动到图示位置（∠aOb＝90°）时，a、b两点间的电势差为（D）

A.√2BRv

B.√2BRv/2

C.√2BRv/4

D.3√2BRv/4

【方法总结】解决电磁感应现象中的电路问题的步骤

（1）“源”的分析：用法拉第电磁感应定律算出感应电动势E的大小，用楞次定律或右手定则确定感应电流的方向，确定电源的正负极，明确内阻r.

（2）“路”的分析：根据“等效电源”和电路中其他元件的连接方式画出等效电路图.

（3）“式”的建立：根据法拉第电磁感应定律并结合闭合电路欧姆定律、串并联电路知识和电功率、焦耳定律等关系式求解.

本文内容由小德整理编辑！