导语：数学推广：数学竞赛中常用的与立体几何有关的12大定理及证明

初高中数学竞赛中涉及到立体几何的公式、定理非常之多，甚至我个人认为无法穷尽。这些定理、公式是数学史上灿烂的瑰宝，但随着时间的流逝及奥数的谈化，这些公式也慢慢谈出了普通初高中生的视野。甚至可以这么夸张地说，现在非常多学生终其读书生涯甚至都没有听说过或者说用到过这些神奇的定理。今天我精选了12个定理来与大家分享，有些给出了证明，有些则没有。但无论哪一种都希望大家应当了解这些定理。

定理1：梅涅劳斯定理及其证明（立体几何中黄金一样的一个结论）

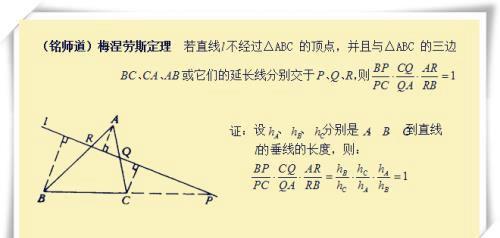
定理2：梅涅劳斯逆定理及其证明（主要用来证明三点共线）

定理3：塞瓦定理（主要用来证明三点共线）

定理4：塞瓦定理的逆定理（证明略）

定理5：角元形式的塞瓦定理（证明略）

定理6：托勒密定理（圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积）及其证明

定理7：三弦定理、四角定理、直线上的托勒密定理及托勒密逆定理（证明略）

定理8：斯特瓦特定理（证明略）

定理9：西姆松定理及其证明（过三角形外接圆上异于三角形顶点的任意一点作三条边的垂线，则三垂足共线）

定理10：九点圆定理（证明略）

三角形三条高的垂足、三边的中点以及垂心与顶点的三条连线段的中点，这九点共圆。

定理11：Stewart定理（证明略）

定理12：欧拉定理及其证明

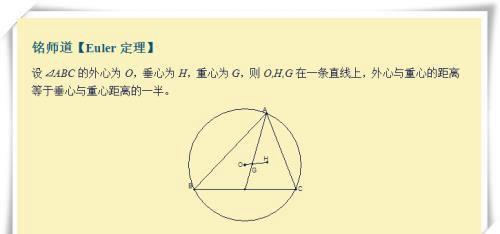
免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小珊创作整理编辑！