导语：高考考纲与考向分析——用样本估计总体

考纲原文

用样本估计总体

（1）了解分布的意义和作用，会列频率分布表，会画频率分布直方图、频率折线图、茎叶图，理解它们各自的特点.

（2）理解样本数据标准差的意义和作用，会计算数据标准差.

（3）能从样本数据中提取基本的数字特征（如平均数、标准差），并给出合理的解释.

（4）会用样本的频率分布估计总体分布，会用样本的基本数字特征估计总体的基本数字特征，理解用样本估计总体的思想.

（5）会用随机抽样的基本方法和样本估计总体的思想解决一些简单的实际问题.

知识点详解

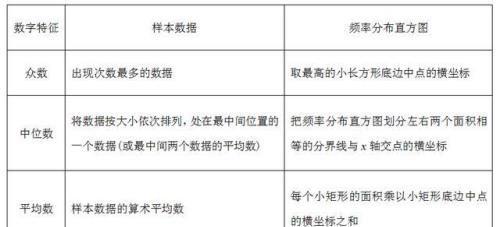
一、数字特征

1．众数、中位数、平均数

2．极差、方差和标准差

极差：即一组数据中最大值与最小值的差．

注：平均数反映了数据取值的平均水平，方差和标准差反映了数据波动程度的大小．标准差、方差越大，数据的离散程度越大，越波动；标准差、方差越小，数据的离散程度越小，越稳定．

3．性质

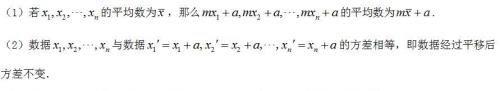
二、茎叶图

1．定义

茎叶图是统计中用来表示数据的一种图，茎是指中间的一列数，叶就是从茎的旁边生长出来的数．

2．表示方法

（1）对于样本数据较少，且分布较为集中的一组数据：若数据是两位整数，则将十位数字作茎，个位数字作叶；若数据是三位整数，则将百位、十位数字作茎，个位数字作叶．样本数据为小数时做类似处理．

（2）对于样本数据较少，且分布较为集中的两组数据，关键是找到两组数据共有的茎．

三、统计表

1．频率分布直方图

（1）画频率分布直方图的步骤

①求极差(即一组数据中最大值与最小值的差)；

②决定组距与组数；

③将数据分组；

④列频率分布表；

⑤画频率分布直方图(以横轴表示样本分组，纵轴表示频率与组距的比值).

（2）频率分布直方图的性质

①落在各小组内的频率用各小长方形的面积表示，且各小长方形的面积的和等于1.

②频率分布直方图与众数、中位数与平均数的关系

a.最高的小长方形底边中点的横坐标即是众数；

b.中位数左边和右边的小长方形的面积和是相等的；

c.平均数是频率分布直方图的“重心”，等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和．

2．频率分布折线图和总体密度曲线

(1)频率分布折线图：连接频率分布直方图中各小长方形上端的中点，就得到频率分布折线图．

(2)总体密度曲线：随着样本容量的增加，作图时所分组数增加，组距减小，相应的频率折线图会越来越接近于一条光滑曲线，统计中称这条光滑曲线为总体密度曲线．

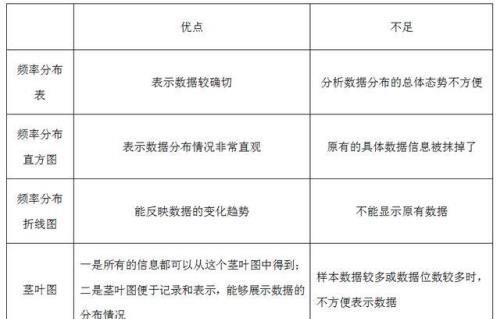
3．各种统计表的优点与不足

考向分析

考向一 数字特征的应用

明确数字特征的意义：

平均数与方差都是重要的数字特征，是对总体的一种简明的描述，它们所反映的情况有着重要的实际意义，平均数、中位数、众数描述其集中趋势，方差和标准差描述其波动大小.

考向二 茎叶图的应用

茎叶图的优、缺点：

由茎叶图可以清晰地看到数据的分布情况，这一点同频率分布直方图类似．它优于频率分布直方图的第一点是从茎叶图中能看到原始数据，没有任何信息损失；第二点是茎叶图便于记录和表示，其缺点是当样本容量较大时，作图较繁琐.

考向三 频率分布直方图的应用

频率分布直方图是用样本估计总体的一种重要方法，是高考命题的一个热点，多以选择题或填空题的形式呈现，试题难度不大，多为容易题或中档题，且主要有以下几个命题角度：

(1)已知频率分布直方图中的部分数据，求其他数据．可根据频率分布直方图中的数据求出样本与整体的关系，利用频率和等于1就可求出其他数据．

(2)已知频率分布直方图，求某种范围内的数据．可利用图形及某范围结合求解．

(3)与概率有关的综合问题，可先求出频率，再利用古典概型等知识求解.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小蔼创作整理编辑！