简题怎么写(简单的小题目)

导语：简炼经典小题简洁巧妙解法“三例”

平面几何中一些看似简单的小问题，却蕴藏着许多奇思妙想。现有三例简炼经典小题，我们一起来想想：

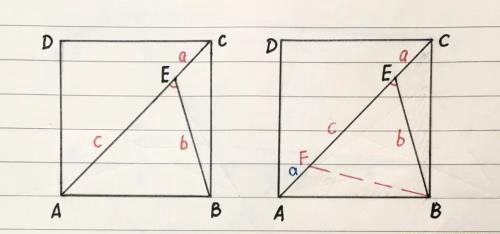
【例一】（如图）正方形ABCD的对角线上一点E，连EB，EA=c，EB=b，EC=a，且a＋b=c，求：∠AEB的度数。

【简解】

（1）在对角线AC上取一点F，使：AF=CE=a，则：EF=c－a=b

（2）△BCE与△BAF中：由已知得：BC=AB，∠BCE=45º=∠BAF，CE=AF，∴△BCE≌△BAF（sAs），∴BE=BF=b=EF

（3）由EF=b=BE=BF，∴△BEF为正三角形，∴∠BEF=60º，即：∠AEB=60º。

【例二】（如图）正七边形，A、B、C、D为其中的四个顶点，且有：AB=a，AC=b，AD=c，求证：1/a=1/b＋1/c

【简解】

（1）由已知正七边形，其必有外接圆（如图）

（2）设另一顶点为E，连AE、BE、CE，由正七边形性质得：AE=BE=AD=c，CE=CA=b

（3）四边形ABCE内接于圆，根据“托勒密”定理：AC·BE=AB·CE＋BC·AE，即：b·c=a·b＋a·c

（4）所以：1/a=1/b＋1/c。

【例三】（如图）在扇形ODE中，∠DOE=90º，OD=9，△ABC是扇形ODE的内接三角形，其中点A、B、C分别在弧DE和半径OE、OD上，∠ACB=90º，AC/BC=3/8，求AC最小值。

【简解】

（1）设：AC=3a，则：BC=8a

（2）取BC中点M，连OM，则MB=MC=OM=4a

（3）连MA，在Rt△ACM中，可得AM=5a

（4）连OA，∴OM＋AM≥OA=9，即：9a≥9，∴a≥1，当A、M、O共线时取等号

（5）故：a的最小值为1，即：AC的最小值为3

以上三例之简解，“道听度说”供参考。

本文内容由快快网络小若整理编辑！