导语：Z变换：与拉普拉斯变换的密切联系；你需要明白的e单位圆

【通信技术基础第10讲】

傅里叶变换建立了从时域到频域的对应关系，拉普拉斯变换建立时域到复频域的对应关系。那么Z变换呢？

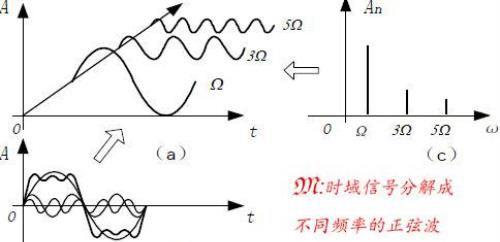
图1：时域与频域

Z变换

如果存在信号x(t)，那么其抽样信号可以表示为周期冲激信号与其乘积。我们再对抽样信号做拉普拉斯变换，得到X(s)。引入一个新的变量z=e^st，那么X(s)可以写成X(z)。

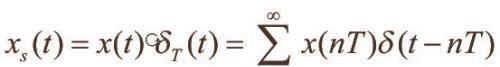
利用拉普拉斯变换公式，求出xs(t)的变换如下：

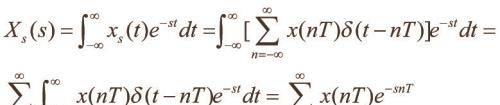
引入一个新的变量z=e^st，那么X(s)可以写成X(z)。OK，Z变换出来了。

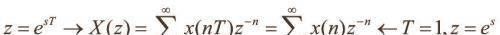
e^ix到底是个什么鬼

不管是傅里叶变换还是拉普拉斯变换，e^ix经常出现，我们在脑海中该如何看待它呢？其实高等数学中的极限章节，说到一个极限,n->无穷，e^x=lim(1+x/m)^n，那么：

有了这个极限表达式，我们可以用Matlab软件去画出e^ix了，只要我们n取的足够大就OK了！当n=50时，为左边黄色图像；当n=500时，为中间红色图像；当n=5000时，为右边绿色图像；可见，当n达到一定值之时，图像上已经显示为一个单位圆了

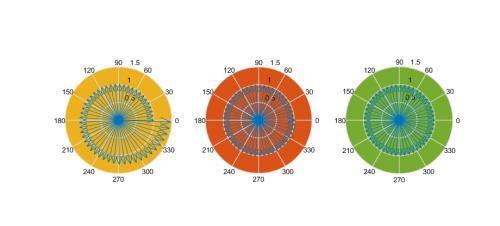
图2：e^ix的图像

将Matlab整个画图过程体现出来，就是从原点开始，“圆规作图”哦。

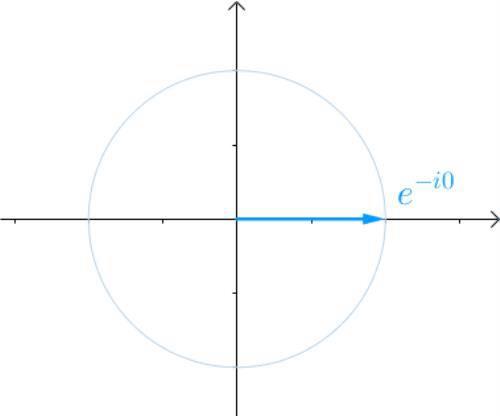
图3 ei的单位圆，这里有个负号，所以从x轴下方开始转

Z变换与拉普拉斯变换的关系

讲到这里，三种变换域方法都涉及了，这些变换并不是孤立的，它们之间有着密切的联系，在一定条件下可以互相转换。下面我们就来看看Z变换与拉普拉斯变换的关系吧。

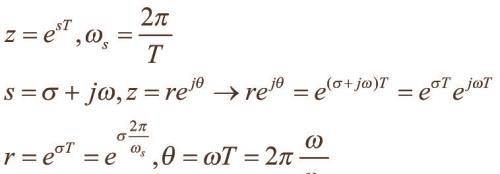
其中T为序列的时间间隔，重复频率为ws=2π/T。可以看出Z平面的半径r与σ有关，而夹角θ与序列的重复频率ws有关。

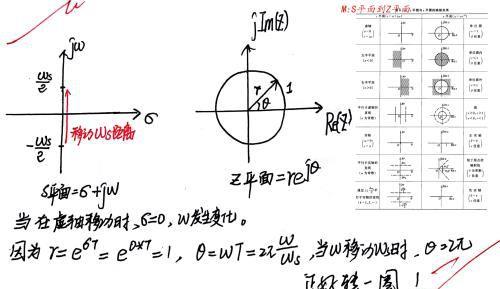
图4：S平面映射到Z平面，其中虚轴的一种情况

当在s平面上，我们放一个蚂蚁在虚轴上，此时无论蚂蚁怎么爬，都爬不出虚轴。这样σ=0，对应在z平面上，r=1，半径固定为1的单位圆；当蚂蚁移动ws个距离之时，根据z平面的夹角θ公式，此时θ转动角度正好等于2π！

所以，在S平面上沿虚轴移动对应于Z平面上沿单位圆周期性旋转，每平移ws，则沿单位圆转一圈。

还有多种有趣的映射关系，比如蚂蚁在实轴上爬呢？各位小伙伴可以自行画图。

总结

当n足够大的时候，e^ix其实就是一个单位圆。并且e^ix代表一族矢量,矢量的角度为x，矢量的幅值为1。我们可以画出经典的图形：

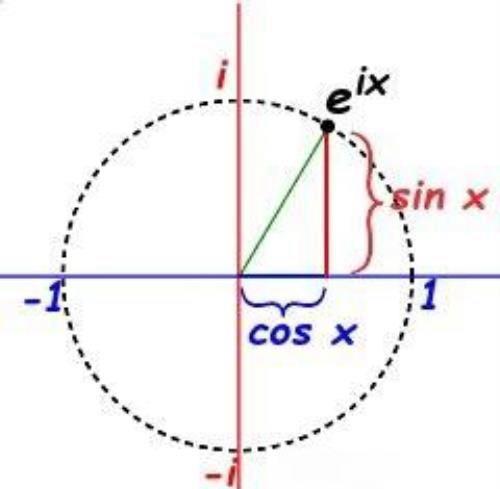
图5：e^ix与欧拉公式

三种变换域存在密切的联系。拉普拉斯变换可以很便捷的解决连续时间系统问题，通过系统函数s域零点、极点分布特性研究系统性能。那么通过s平面与z平面的关系，我们容易用类似的方法研究离散时间系统的系统函数z平面特性与系统时域特性、频响特性以及稳定性的关系。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小德创作整理编辑！