导语：多项式乘法、十字相乘法与三位数的乘法

十字相乘法的实质是多项式的乘法，一个三位数也可以写成多项式的形式，所以两个三位数的乘法，可以利用多项式的乘法横向展开来做，还可以利用十字相乘法列竖式划十字来做。本文只是在初中学过多项式乘法和十字相乘法之后，回头再验证小学数的乘法法则的正确性，以及多项式的乘法与十字相乘法在具体应用方面做一点探讨，给学生和数学爱好者提供一个看问题的视角，绝无意取代小学所学的方法，特此说明。

一。多项式乘法与三位数的乘法

设两个三位数分别为100a+10b+c，100d+10e+f，为说明简便计，以下我们把三位数的百位，十位，个位，分别简称为首，中，末。则

(100a+10b+c)(100d+10e+f)=ad10^4+(ae+bd)10^3+(af+be+cd)10^2+(bf+ce)10+cf,

观察发现，展开后的结果由五部分构成：

ad10^4，(ae+bd)10^3，(af+be+cd)10^2，(bf+ce)10，cf。

其中ad，cf分别为首首相乘，末末相乘，

ae+bd，是首中相乘再相加，

bf+ce，是中末相乘再相加，

af+be+cd，是首末相乘，中中相乘，再相加。

而系数10^4,10^3,10^2,10^1,10^0,可以看作起占位作用。

因而，三位数乘法的横向展开：

(首，中，末)(首，中，末)=(首首，首中交叉乘加，中中+首末交叉乘加，中末交叉乘加，末末)

例题1：291×435

(291)(435)=(8，42，41，48，5)

=8×10^4+42×10^3+41×10^2+48×10+5=126585,

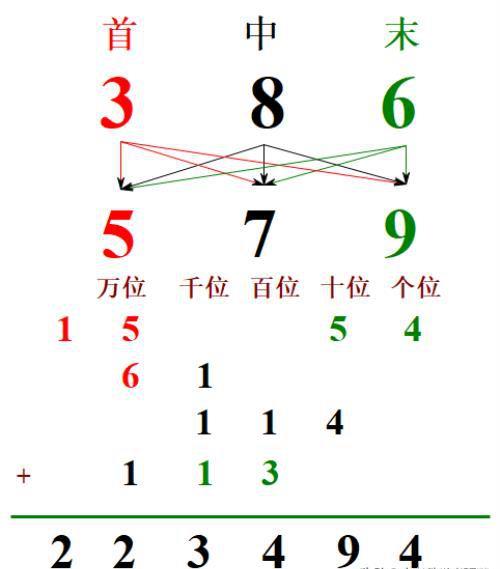
例题2：386×579

(386)(579)=(15，61，113，114，54)

=15×10^4+61×10^3+113×10^2+114×10+54=223494,

至此，可以看出利用多项式的乘法，能够把三位数的乘法横向展开。

二。十字相乘法与三位数乘法

十字相乘法，列竖式，划十字；先求积，再累加。求积容易累加难，难在弄清数位，对齐累加。

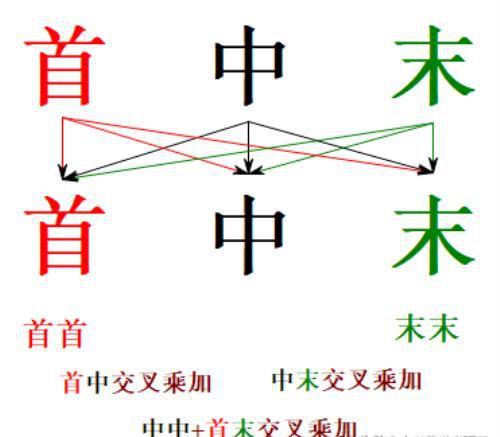
用十字相乘法尝试例题1：291×435

由前面的分析，我们知道(291)(435)=(8，42，41，48，5)。

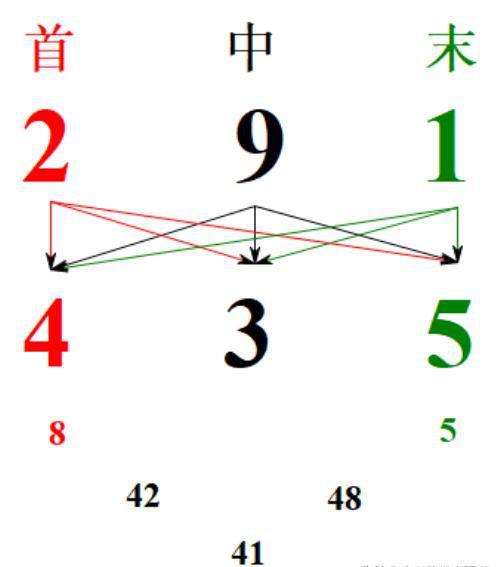
因为两个三位数相乘的结果，最大是一个六位数(999×999=998001)，关键是要清楚：8，42，41，48，5，这五部分在结果中所处的数位。

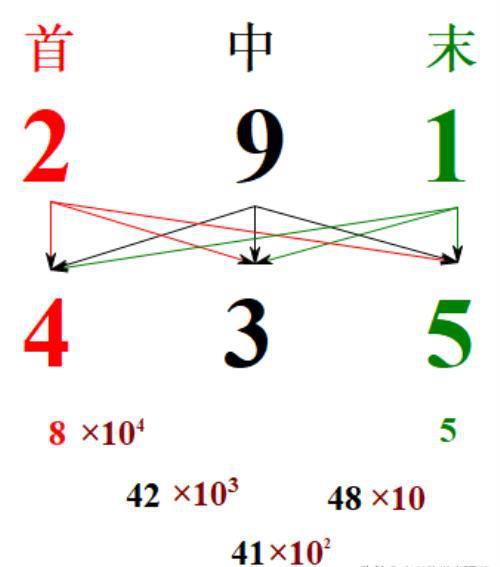
因而，

8，实际表示8万，8在万位，

42，实际表示4万2千，4在万位，2在千位，

41，实际表示4千1百，4在千位，1在百位，

48，实际表示4百8十，4在百位，8在十位，

5，实际表示5个，5个个位。

位数相同的数字累加，万位累加8+4=12，千位累加2+4=6，百位累加1+4=5，十位8，个位5，

最终结果126585。

在竖式中，以数位相同对齐的方式呈现如下：

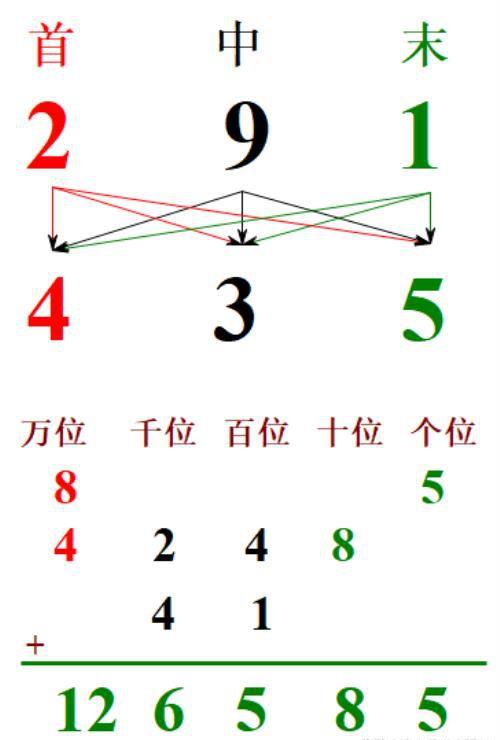
用十字相乘法尝试例题2：386×579=223494

(386)(579)=(15，61，113，114，54)=(15万，61千，113百，114十，54个)

例题3：479×365

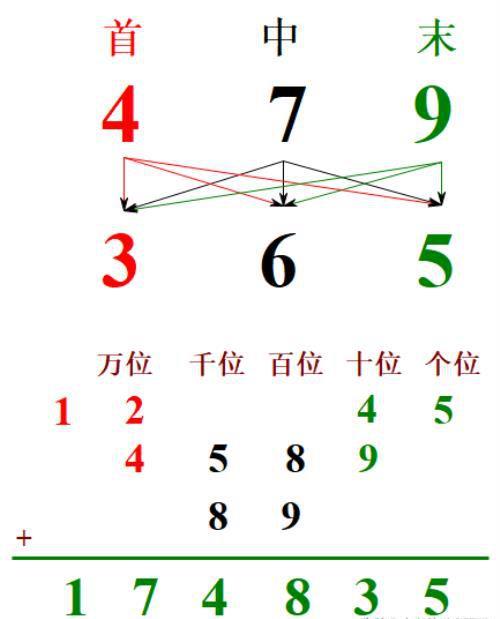
由此可见，小学所学列竖式做乘法：用一个因数各数位上的数字去遍乘另一个因数各数位上数字，与两个多项式相乘，用一个多项式的每一项去遍乘另一个多项式的每一项，是同样的道理。或者说，初中多项式的乘法就是小学多位数的乘法的理论基础。小学生只知道法则，不知道法则背后的数学原理，进入初中以后就可以明白这其中道理，并促进他们由操纵数的运算过渡到操纵字母的运算。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑！