射频电路中的共轭阻抗匹配介绍图(共轭阻抗匹配的作用)

导语：射频电路中的共轭阻抗匹配介绍

从前面的章节中的讨论可以看出，电压或功率反射对数字或射频电路的性能非常有害。电压和功率反射都是由于源或负载中存在不匹配的阻抗条件所造成的。阻抗匹配因此成为包括射频、数字和模拟电路在内的所有电路设计中的一个关键课题。

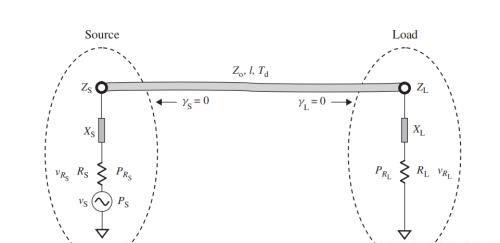
最大功率传输

首先，让我们讨论从一个源到一负载没有反射情况下的功率传输的情况，即如图1所示：

图1

图1 当γS=0，γ L =0时以及当l<<λ/4时，所以Td →0，功率无反射地从源传输到负载；

从源到负载阻抗实部RL的电压和功率可以用下面的方程表示：

对于射频功率传输，最好实现从源到负载电阻之间的最大功率传输。从上面的表达式中，很容易看出，如果表达式中的分母达到最小值，那么表达式的值则将达到最大值。分母中的两个项不能是负的，但必须是正的或零的，因为它们是实值的平方。理论上，最小的可能值为零。而分母中的第一项是电阻值的项，因此不能为零。但是，分母中的第二项可以被强制为零，即：

另外，上面的关系式表明源和负载的电抗必须具有相等的大小，但是具有相反的符号。它意味着负载电抗X L 必须是感抗，如果源电抗X S 是容抗的话，反之亦然。根据上面的各个关系式可以推导出负载上接收到的功率为：

现在，从方程上面的方程中可以找到实现从源到负载电阻的最大功率传输的另一个关系。在数学上，通过对上面的负载电阻上接收到的射频功率对负载阻抗部分RL取偏导得到：

而使负载阻抗上的功率最大化的条件是：

根据上面的关系式，我们有：

结合各个方程我们得到的是所谓的阻抗共轭匹配条件或简单的阻抗匹配条件，如下面的方程所示：

2.4.1 没有相移的功率传输

图2

图2 当源的电抗被负载的电抗“中和”时，两种匹配的情况，反之亦然，即XS =−XL 。 (a)RS与XS串联RL 与XL串联。 (b)RS 与XS并联， RL 与XL并联。注：当L<<λ/4时，T d →0.

上面的最大功率传输条件表明，当源和负载的电抗，即XS 和XL分别被彼此中和后，然后图1所示的示意图可以重新绘制，如图26所示。在从源到负载的整个回路中，只有电阻部分，没有电抗部分。这意味着当电压或功率从源传输到负载时，没有相移，即：

其中符号“∠x”表示角度x。

总之，阻抗共轭匹配的意义体现在以下两个方面：

1. 最大限度地实现从源到负载之间的功率传输；

2. 将电压从源端传输到负载端时不会发生相移。

对于上面的第二点，即没有相移的电压或功率传输，是阻抗共轭匹配的另一个重要特征。遗憾的是，在关于阻抗共轭匹配的讨论中，它经常被忽略或神秘地“消失”。在过去的几十年里，调制技术得到了长足的发展，

图3

图3 从PSK到QAM的调制技术发展： (a)BPSK，(b)4PSK，(c)8PSK， (d)16PSK，(e)16QAM，(f)64QAM。

相位调制对频率带宽的有效利用起着重要的作用。图3说明了通信系统中调制技术的进展.. 历史上，PSK（相移键控）技术从BPS K（双相移键控）发展到QPS K（四相移键控）、8PSK、16PSK等。在16PSK系统中，如图3(d)所示，两个相邻符号点之间的最小相位差只有22.5◦ 。这是电路设计者面临的一个难点。与PSK系统不同，QAM系统大大增强了识别相邻两个符号之间的分辨率。在QAM系统中，振幅和相位都被应用于符号的分配，以便系统不仅通过其相位识别符号，而且通过其振幅来识别符号。它放宽了两个相邻符号之间的相位差要求。在16QAM系统中，相邻两个符号之间的最小相位差是26.37◦，如图3(e)所示，而在16PSK系统中，这个值大于22.5◦ ，如图3(d)所示。为了进一步提高带宽利用率，在16QAM系统之后研究者又开发出64QAM系统甚至256QAM系统。当然，相比16QAM系统64QAM是一个更复杂的系统，在64QAM系统中两个相邻符号之间的最小相位差为9.46◦ ，这对射频电路设计者是一个很大的挑战。

现在，让我们回到阻抗共轭匹配的话题。

从上述讨论中可以清楚地看出，如果源和负载的阻抗不匹配时，则从源到负载的回路中将会存在相移。如果相移是不稳定和可变的，那么它会使设计的射频模块或者系统无法工作。如前所述，64QAM系统的最小相位差仅为9.46◦ 这是整个系统能够容忍的相移的上限。对于单个RF块，相移变化的误差必须小于9.46◦ 。因此，在射频电路设计中，阻抗匹配是绝对必要的。

在前面推导出来的阻抗共轭匹配的条件下，可以得到负载处的最大功率，如下面的方程所示：

类似于功率传输表达式，电压vRS信号其在源电阻R S上相应功率为PRS，可表述如下：

通过将阻抗共轭匹配条件代入上面的方程，我们得到了：

从这些方程中，我们可以根据阻抗共轭匹配的条件下得出以下结论：

l 传递给负载的功率达到最大值；

l 传递给负载的功率等于源处剩余的功率。

相应的方程式是：

在从源到负载的循环中，可用总功率PS 等于 RS和R L上的功率之和；

总功率分为两部分：总功率的一半仍在RS，而另一半被被送到了负载R L1.

本文内容由小楠整理编辑！