隐圆问题(隐圆问题的4种模型)

导语：隐圆与圆幂定理应用题3例

隐圆与圆幂定理应用题3例

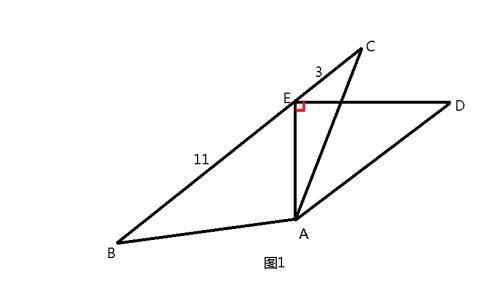
题目1：如图1，三角形ABC和直角三角形AED中，E是BC上一点，BE=11，CE=3，AB=AC=AD，求ED的长度（√33）。

解题思路：见图2，题目已知三条相等线段共端点，可想到隐圆问题；题目还告诉两条已知长度线段，求另一条与之相交的线段长度，可用相交弦定理解决。

先作以A点为圆心，AB为半径的圆。已知AE⊥ED，利用垂径定理性质延长DE至F，显然EF=ED，

EF·ED= BE·CE，即可求出ED长度为√33。

题目2：过ABC的重心G及顶点A作圆与BG切于G，CG的延长线交所作圆于D。

求证：AG²=GC • GD。

解题思路：本题要证明三条线段（共端点）之间的关系，其图形结构可联想到相交弦定理；G点为重心，三角形底边为中点，可想到中位线性质或倍长中线。

如图2，过C作CF∥BG交AG延长线于F，因为AK=KC，所以AG=GF。 连接AD，因BG是圆的切线，故∠ADG=∠AGK=∠AFC=α（弦切角定理），于是A、D、F、C四点共圆，根据相交弦定理得AG•GF=GC•GD，以GF代AG，AG ² =CG • GD成立。

题目3：如图，过正方形ABCD的顶点A作一直线分别交BD、CD及BC的延长线于E、F、G，圆0是△CGF的外接圆，求证：CE和圆O相切。

解题思路：欲证明EC与圆相切，连接OC，证明OC⊥EC即可（详见应用正方形对角线上点的性质解题5例）；或证明EC²=EF·EG（切割线定理的逆定理，△EFC∽△ECG即母子相似）；或弦切角定理的逆定理（∠DAE=∠DCE=∠G）等三种方法。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小欣创作整理编辑！