初中数学旋转动点专题(动点旋转问题综合题)

导语：一道旋转和动点问题等结合的中考数学真题

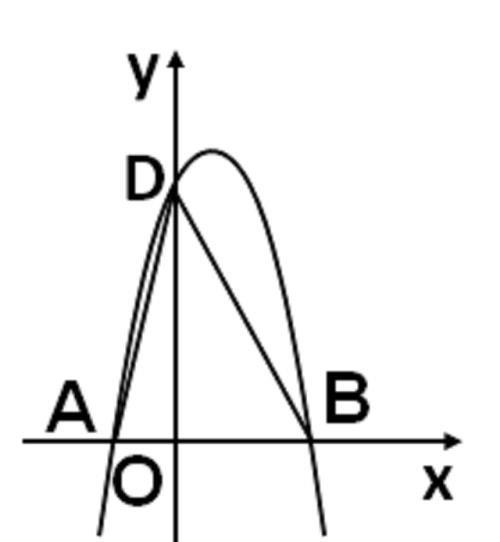
如图, 坐标平面内, O为坐标原点, 抛物线y=ax^2+bx+c与x轴交于点A(-1,0), B(2,0), 与y轴交于点D, 已知tan∠DAO=4.

(1)求D坐标及抛物线的解析式；

(2)将△OAD绕平面内某点顺时针旋转90后使△OAD的两个顶点落在抛物线上, 求旋转后O点的对应点的横坐标；

(3)在BD上方的抛物线上找一点P, 使∠PDB=2∠ODA, 求P点横坐标.

解：(1)∵tan∠DAO=OD/OA=4, （正切的定义）

∴OD=4OA=4.

c=4, D(0,4).

c/a=-2, a=-2;-b/a=1, b= 2;

(一元二次方程根与系数的关系)

抛物线的解析式为：y=-2x2+2x+4

(2)记旋转后对应三角形为△O’A’D’, 设O’的横坐标为z,

若A’, D’落在抛物线上,可记A’(m, -2m2+2m+4), D’(n, -2n2+2n+4),

则n-m=4,

(-2m2+2m+4)-(-2n2+2n+4)=1,

解得：m=-23/16,

则：z=m=-23/16,

若O’, D’落在抛物线上,则

n-z=4, n+z=1,

解得z= -3/2,

∴O点的对应点的横坐标为-23/16或-3/2.

(3)设P点的横坐标为p, 作∠BDE=2∠ODA, 使DE=BD,

且DE交抛物线于P,

AD=√17, OA=1, DE=BD=2√5,

过D作BE的垂线段DC，则△AOD∽△BCD

BC=OA·BD/AD=2√5/√17,

BE= 4√5/√17,

设E(x, y), 则(x-2)2+y2= 80/17, x2+(4-y)2= 20,

舍去不合理的值，解得：x=62/17, y=24/17,

lDE: y=-22x/31+4

当-2x2+2x+4=-22x/31+4, 即-2x2+84x/31=0

∴p=42/31.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小面创作整理编辑！