有效应力原理在岩土工程中的应用论文(有效应力原理在岩土工程中的应用研究)

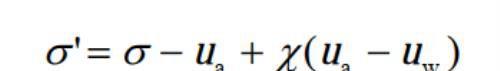
导语：有效应力原理在岩土工程中的应用

有效应力原理在岩土工程中的应用

饱和土的有效应力原理是太沙基在发表固结理论时提出来的，有效应力原理的提出，阐明了松散的土体材料与一般固体材料的本质区别，使得土力学从固体力学脱离出来，成为一门独立的学科。同时，有效应力原理的提出，也奠定了现代土力学变形与强度计算的基础。该原理认为：施加于饱和土体的总应力可以分为两部分，一部分由孔隙水承担，称为孔隙水压力，另一部分由土骨架承担，称为有效应力。需要指出的是：有效应力是虚拟的，并不等于土颗粒接触点竖向应力的统计平均值，理解有效应力，应从土骨架的变形与强度等效上去理解，有效应力实质是一种等效应力。有效应力原理阐述了饱和土体内部受力和传力机制，在总应力不变的前提下，有效应力和孔隙水压力既共同承担又相互转化。该原理可表述为：

（1）饱和土体内任意平面上受到的总应力σ等于有效应力σ＇与孔隙水压力u之和。

（2）土体的强度与变形只取决于有效应力，与孔隙水压力无关。

非饱和土的有效应力原理由于孔隙气压力的存在相对复杂，而且估计和测定空隙气压力也有很大的难度。相对而言，非饱和土的有效应力原理远不如饱和土有效应力原理成熟。目前，非饱和土的总应力、有效应力和孔隙压力一般由毕肖甫建议的公式来描述：

介于0-1之间，对于饱和土，χ=1，毕肖甫有效应力原理退化为太沙基有效应力原理，对于干土，χ=0。

在非饱和土力学中，

称为基质吸力，是一个非常重要的概念。

前面指出，有效应力作为一种虚拟应力，并不能直接量测，因此要确定有效应力的大小，需估计和计算孔隙水压力的大小。

对于饱和土体，在简单受力状态下（一维竖向应力状态），施加荷载的瞬间，总应力全部由孔隙水压力承担，即σ=u

对于复杂应力状态，例如轴对称二维主应力增量组合作用下，斯肯普顿基于常规三轴试验提出孔隙压力增量公式：

式中：A、B为孔压系数，其中系数B与土体饱和度有关，介于0-1之间，系数A并不是一个常数，与剪切时土体体积变化有关，如果将土体视为线弹性体，A=1/3。

在基坑工程中，主动区土体处于侧向卸荷状态，竖向应力保持不变，即Δσ1=0，Δσ3=Δσc ，应采用减围压三轴压缩试验来模拟。此时孔隙水压力 Δu=BΔσc (1-A)

基坑底部土体处于侧向应力保持不变，竖向应力减小状态即Δσ1=Δσc ，Δσ3=0，应采用三轴伸长试验模拟。此时孔隙水压力

Δu=ABΔσc

在非对称空间应力状态作用下，考虑中主应力σ2的影响，汉高引入八面体应力，提出更一般化的八面体应力公式：

有效应力原理的重要性已逐渐被人们所认识并已引起足够的重视，因为它不同程度地贯穿于土力学学科的各项内容，有效应力原理的提出，促进了土力学解决工程问题的发展，它的提出与应用，使土力学有了自己特定的理论原理，使得土力学区别于一般的固体力学。

土体的固结理论应该是有效应力原理中孔隙水压力与有效应力分担与转换最直接的体现与应用，是固结理论建立的基础。土力学中土体的抗剪强度的不同测定方法及其相应指标的产生则是有效应力原理对经典强度理论和破坏准则的具体描述。由于有效应力下强度指标不依赖于应力路径，具有相对稳定的特点，因而认为有效应力下的强度指标反映了土的固有性质，由此引出了基坑支护设计中有效应力法，支护结构上土压力的计算采用水土分算就是有效应力原理运用的又一实例。必须指出的是，采用水土分算计算土压力的强度指标应采用有效应力下的强度。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小奈创作整理编辑！