求阴影面积竞赛题(小学数学六年级竞赛题库求阴影面积)

导语：求阴影面积，迎春杯六年级决赛题

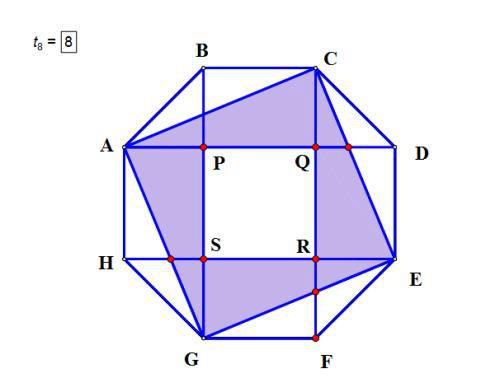
如图正八边形ABCDEFGH的面积是1，其中有两个正方形ACEG和PQRS．那么正八边形中阴影部分面积是多少？

显然，这样阴影部分面积的题目一般不会直接去计算

咱们可以考虑阴影面积常用的方法，比如辅助线法、相加或相减法、割补法、平移、旋转等首先观察分析：根据条件，我们可以把阴影部分面积可以分成四个规则且相等的直角三角形

但每个三角形所在的梯形面积不好计算，缺了一个角，我们看缺的这个角又比较特殊--相同的“等腰直角三角形”。

我们再看条件，这是一个正八边形，中间有小正方形PQRS，容易得出小正方形的边长和正八边形的边长是一样的（如PQ=CD）“小正方形，四个等腰直角三角形”，如果把中间小正方形对角线边起来我们将会得到

正好分成四个相等的等腰直角三角形，把这四个三角形移出去分别补上，（如三角形POQ补到CD处）斜边重合。

再去掉一些线段，我们就可以得到如下图形

每个直角三角形正好是所在长方形的一半，根据等积变形，四个长方形的面积之和正好是原来正八边形面积所以阴影部分面积是: 1/2小结：本题是一个较典型的等积变形问题，阴影面积划分以后可以成为规则图形，充分利用所给的正八边形，正方形等条件，结合图形进行观察分析，找到突破口，化不规则为规则，从而解决问题。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小珊创作整理编辑！