> 动物

k近邻算法是有监督还是无监督(k近邻算法的优缺点)

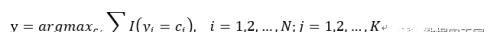
导语：k近邻算法

从今天开始，我们将介绍机器学习中的分类模型。首先要登场的就是我们的k近邻（k-nearest neighbor，k-NN）算法。

首先要说明的是，k近邻既可以用来分类，也可以用来做回归。我们这里只介绍它的分类用法。

1 原理

我们先来说明下k近邻算法的细节：

第一步，给定一个训练数据集。然后对于新的样本x，在训练集中找到与x最近邻的k个点。

第二步，找到k个点中出现类别次数最多的那个类，就把x归为这个类。用数学公式表达就是：

其中，i的取值从1到N，代表训练集的样本数；j的取值从1到k，代表训练集中的类别数。I是指示函数，含义是当y=c是，I为1，否则I为0。

举个例子来说明上面公式的含义：

假设我们找到了与x最近的5个点，其中3个为c1类，2个为c3类。不妨再假设y1，y2，y5是c1类，y3，y4是c3类。这样，对于c1类来说，y1=c1，y2=c1，y3≠c1，y4≠c1，y5=c1。所以I(y=c1)的值为3，同理，I(y=c2)的值为2。因此，返回的结果是值为3对应的类别c1，即x的类别为c1。

这就是k近邻算法的步骤，是不是感觉很直接呢？

2 调参

注意k近邻的第一步，找到x的最近邻。那么这个近邻怎么衡量呢？一般我们用Lp距离来衡量。两个向量x1，x2的Lp距离可以定义为：

其中，当p=2时，叫做欧式距离，就是平常求的平方根。当p=1时，叫做曼哈顿距离，就是求绝对值。

还有一个关键参数是k近邻中的k。我们到底选k为多少合适呢？如果k值过小，新样本选择的范围就小。只有与新样本很近的点才会被选择到，那么模型就比较复杂，容易发生过拟合。如果k值过大，新样本选择的范围增大，那么模型就会变得简单，容易发生欠拟合。举个极端的例子，如果k的值是整个训练集的样本数，那么返回的永远是训练集中类别最多的那一类，也就失去了分类的意义。

3 效率

从上面的描述中不难看出，k近邻算法在实现时，要计算新样本与训练集中每一个实例的距离。这种线性搜索会大大增加时间的消耗，尤其是在数据集相当大的情况下。

为了提高效率，有种叫做kd树的方法就可以实现。kd树的内容我们简单介绍下，它是一种二叉树，主要是按训练集数据的不同维度的中位数来划分区域。具体的原理就不详细解释了，我们只要知道它的速度很快就可以了。

好了，这就是今天的全部内容，下期再会。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑！