如何用三角函数证明勾股定理(如何用三角函数证明勾股定理公式)

导语：如何用三角函数证明勾股定理？

林朝夕同学，在这漫长而美好的一生当中，只要你认真想做一件事情，不论从什么时候开始，都不算晚！

——《天才基本法》

看问题有多种角度。例如对于三角恒等式sin² α+cos² α=1，我们用熟悉的勾股定理的角度看，可以把二者用等号连接。常常认为是可以用勾股定理证明这个重要的三角恒等式。

但是，我们要讨论的是不使用勾股定理，而是用三角函数给勾股定理的400多种证明方法再增加一种证法。

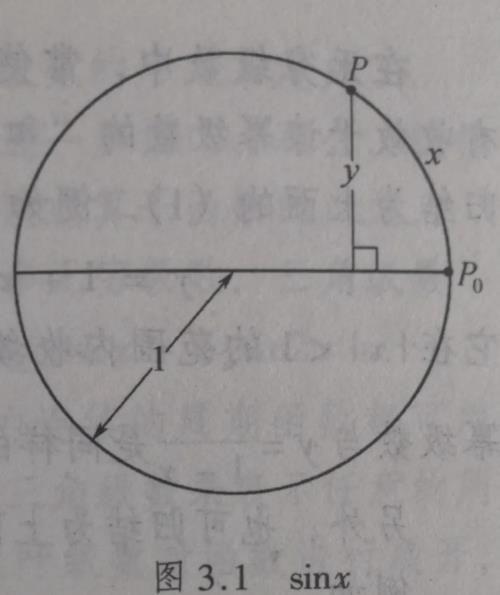
从预备知识讲起

我们用图形来辅助说明正弦函数的定义:假设从单位圆(半径为单位长度即1的圆)的圆周上一点p₀出发，沿着圆移动了x这一角度后得到点p，从p到p₀所在的直径作的垂直线为y。

由于实数y随着实数x的确定而确定，所以y是x的函数。这是一个常见的重要的初等函数，约定一个符号比较方便。由于历史的原因，我们约定:这个关系就表示为

y=sin x

与此类似，其余的三角函数，即“实数→实数”的对应若被定义了，那么，各自特别的函数符号也就被定义了。

接下来，我们看看锐角三角函数。请看下图:

上图介绍了6个三角函数，其实重要的只有3个，即正弦函数、余弦函数和正切函数。在科学计算器上，只有上面的3个函数才找得到按键。

欧拉是用单位圆上的函数线来定义三角函数的。请看下图:

单位圆的圆心位于平面直角坐标系的原点，单位圆与x轴交于点A和点A&39;。角α的始边在x轴上，终边与单位圆和过点A的单位圆切线分别交于点p和点T。

用函数线来定义，结果如下:

sin α=MP(正弦线)

cos α=OM(余弦线)

tan α=AT(正切线)

把上面这三个三角函数所表示的三角形两边之比写出来:

正弦=对边比斜边

余弦=邻边比斜边

正切=对边比邻边

再仔细对比，就会发现三者中的任意两个，都分别共有一条边。这也暗示我们，三者之间肯定存在密切关系。

事实就是如此，请看下面非常重要的两个基本公式:

(1) sin² α+cos² α=1

(2) tan α=sin α÷cos α

怎么证明公式(1)呢？公式(2)可以用函数的定义推导出来，公式(1)的证明请看下一个单元。

用勾股定理证明公式(1)

先从简单的证明方法开始，下一个单元讲勾股定理的三角函数证明方法。

从勾股定理出发，可以推导出公式(1)，过程请看下图:

(1)式是勾股定理。把(1)式两边同时除c²，得到(3)式。(4)式是课本上的定义，代入(3)式，得到公式(1)。

预备知识:用圆内的弦定义正弦

有人想知道正弦的名字从何而来？下图所示的正弦函数的定义是合理解释。

在直径为1的圆中，圆周角α所对的弦长，叫做角α的正弦，记作sin α。

如图所示，弦BC是圆周角α的正弦，弦CD是圆周角β的正弦。

因为在同圆内，相等的圆周角对等弦，所以这个定义是合理的。根据这个定义，我们可以推导出正弦函数的性质以及正弦定理和一系列的三角恒等式。

上图所示的圆内接四边形有很多重要的几何性质。例如，对角互补，连接两条对角线，可以构造出两对相似三角形，等等。

正弦和角公式的证明

现在我们用上图来证明正弦和角公式:

α和β为锐角时，

sin(α+β)=sin αcos β+cos αsin β

因为四边形ABCD的外接圆直径为1，所以有

sin(α+β)=BD=BE+ED

=BCcos β+DCcos α

=sin αcosβ+cos αsin β

三角函数的诱导公式:

sin α=cos(90°-α)

cos α=sin (90°-α)

需要死记硬背吗？不需要。它告诉我们，角α的余角的正弦称为余弦，正弦函数和余弦函数互为余函数。

在纸上画个直角三角形，标出a，b，c，用正弦和余弦的定义就能够推导出来。

勾股定理的三角证法

根据上面的诱导公式和正弦和角公式，我们取α+β=90°的特例，就能够推导出公式(1)。

sin(α+β)=sin 90°=1

=sin αcos β+cos αsin β

=sin αcos(90°-α)+cos αsin(90°-α)

=sin² α+cos² α

即公式(1):

sin² α+cos² α=1

请注意，上述论证没有使用勾股定理，而是用三角函数证明了勾股定理。

因为函数线PM，OM，OP构成了直角三角形，PM=sin α，OM=cos α，OP=1，所以，证明了公式(1)就等价于证明了勾股定理。

总结

值得注意的是，我们前面论证正弦和角公式的时候，并未像通常教科书上的证明那样要求α+β为锐角。事实上，上述论证可以推广到α+β在0°到180°之间的一般情况。

而且正弦差角公式的证明方法类似。请看下图:

只要注意到

sin(α-β)=CD=DE-CE

即可。

正弦和差角公式具有重要的意义，是必须彻底掌握的公式。

有了正弦和差角公式，就可以编制正弦函数表，推导出其它三角公式，推导出各种诱导公式。

诱导公式

上图所示是各种诱导公式。竟然有那么多很容易混淆的公式！现在你大概会明白为什么很多人在学三角函数这部分时有一种挫败感。

所以，千万不要死记硬背。这些公式都能用正弦和差角公式推导出来。

还有一种方法是按照欧拉的任意角三角函数的定义，在纸上画平面直角坐标系和单位圆，自己推导。详情请大家看曹奂东的追光课堂。

要学会通过不同的方法解决问题。

科学尚未普及，媒体还需努力。感谢阅读，再见。

本文内容由快快网络小媛整理编辑！