三角形中间一点求角度(三角形的中点怎么算)

导语：三角形给出中点和角度求其他角度的问题

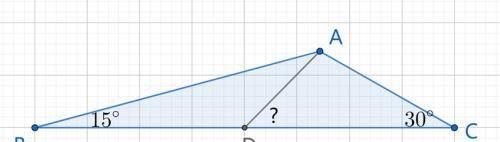
如图，△ABC中，D是BC中点，∠ABD=15°，∠ACD=30°，求∠ADC的度数。

这道题给出的是特殊角，其实不论用什么辅助线构造直角三角形，慢慢算都可以算出来的，因为特殊角的三角函数都是已知的。因此，只要能够构造出直角三角形，题目就能解得出来。

但是通过这道题目，可以锻炼思维，因为这道题目的条件非常典型，下面记录几种比较直观的思考方法。

1.做辅助线将15°角翻倍成30°角，形成等腰三角形

做BE，使∠EBA=15°，这样形成等腰△EBC。连接ED，则ED⊥BC。

现在有等腰△EBC，BA是∠EBD的角平分线，又有30°角的直角三角形，于是可以按照图中所示，逐步计算各条需要计算的线段长度。

这里还使用到了“角平分线定理”，计算出EA和CA的长度。

最终，回归到待求解线段所在三角形ADC中，确切地说是回归到三角形ADF中。通过特殊角从而计算出线段长度，进而求出∠ADC的值，结果为45°，因为可以计算出AF=DF。

【思路总结】有倍角关系时，可考虑做倍角形成相等角度，进而形成等腰三角形。

2.延长CA形成直角三角形

做BE使得∠EBA=45°，与CA延长线相交于E，这样形成直角△BCE。

D又是斜边中点，可以利用直角三角形斜边中线等于斜边长一半的性质，同时△EBA又是等腰直角三角形，于是可以按照图中提示解出△ADF中各条线段的长，最后计算得∠ADC=45°。可以注意到，目标是计算∠ADC的角度，因此这个方法最终也是回到△ADF的计算。

还有另外一个巧妙的办法，就是利用边长的关系直接进行角度的计算。

如图所示，构造出的三角形全部都是极其特殊的三角形，因此可以直接计算角度。

【思路总结】有中点时，可以考虑以给出中点的边为斜边，做直角三角形，利用直角三角形斜边中线等于斜边长一半，同样可以构造出等腰三角形。

3.直接过A做AF⊥BC，解三角形

通过前面两个方法可以看到，要求∠ADC的度数，最终一定是要回归到这个角度本身所在的三角形。于是可以直接做AF⊥BC，但是这样没法直接求出∠ADC的值。我们可以看到，△ABC左边底角15°和右边底角30度成2倍角关系，那么可以做一条辅助线形成两个等腰三角形，如下图所示。这样，可以分段计算BE、ED、DF、FC的值，于是可以求得∠ADC。个人认为这是最直接的方法，基本不需要技巧。

【思路总结】三角形两个角度是倍角关系时，像本方法中的辅助线构造两个直角三角形是最常用的一种做辅助线的方法，一定要领会。

4.利用三角形外接圆求解

还可以做△ABC的外接圆，利用圆心与各个顶点之间连线的关系计算。

5.利用正弦定理解三角形

使用正弦定理解这道题是代数方法中最直观的方法，只要有熟练的三角函数基本功，都可以得到结果。

本文内容由小萱整理编辑！