并查集面试(收集面试官资料)

导语：高端面试必备：并查集

并查集 (union & find) 是⼀种树型的数据结构，⽤于处理理⼀些不交集(Disjoint Sets)的合并及查询问题。

一般有2个操作：

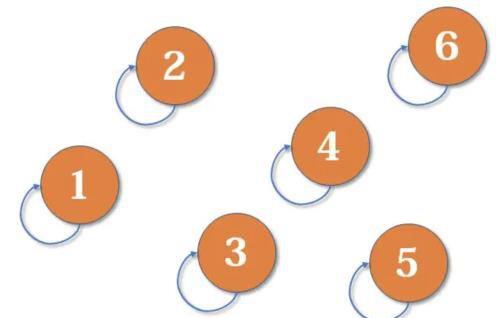
Find： 确定元素属于哪⼀个⼦集。它可以被⽤来确定两个元素是否属于同⼀子集。Union:将两个子集合并成同⼀个集合。算法核心思想

（1）最开始时候，每个元素构成一个集合，起parent就为元素本身

（2）1和3元素合并

（3）2和3合并

（4）4、5、6元素合并

（5）1、2、3 和 4、5、6元素合并

代码最简单的并查集代码

class UnionFind {    int[] parent;      public UnionFind(int n) {        parent = new int[n];        for (int i = 0; i < n; i++) {            parent[i] = i;        }    }  public int find(int x) {        if (parent[x] == x) {            return x;        } else {            return find(parent[x]);        }    }    public void union(int x, int y) {        int i = find(x);        int j = find(y);        if (i == j) {            return;        }        parent[i] = j;    }}

改进一下：在实际的合并过程，往往会出现如下图情况，形成以及链式集合，这样查询的时候效率很低，parent数组存放了太多的无用信息，其实我们只需要关注的就是根节点信息就可以了。

我们用一个数组rank[]记录每个根节点对应的树的深度（如果不是根节点，其rank相当于以它作为根节点的子树的深度）。一开始，把所有元素的rank（秩）设为1。合并时比较两个根节点，把rank较小者往较大者上合并。

class UnionFind {    int[] parent;    int[] rank;      public UnionFind(int n) {      parent = new int[n];      for (int i = 0; i < n; i++) {          parent[i] = i;      }      rank = new int[n];      Arrays.fill(rank, 1);  }      public void union(int x, int y) {      int i = find(x);      int j = find(y);      if (i == j) {          return;      }      if (rank[i] > rank[j]) {          parent[j] = i;      } else {          parent[i] = j;      }      if (rank[i] == rank[j]) {          rank[i]++;      }  }}

本文内容由快快网络小媛整理编辑！