决策树解决的问题(决策树常用来解决什么问题)

导语：五分钟了解决策树智能算法

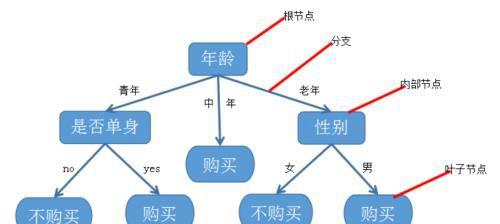
决策树（decision tree）算法是机器学习中的一个重要算法，因为它是很多其他智能算法的基础。决策树是一个类似于流程图的结构，因像一棵树而得名。决策树包含：

1.根结点，最顶层的那个结点；

2.叶子结点，每条路径最末尾的结点，也就是最外层的结点，代表类或类分布；

3.内部结点，一些条件的结点，下面会有更多分支，也叫做分支结点，表示对一个属性的测试，每个分支代表一个属性输出。

例如下图：

图一

怎么才能构造出上面的决策树呢？我们通过一个实例来认识决策树！并构造出决策树。

第一步：收集信息。某饭店对某种美食套餐的潜在顾客进行了调查，得到以下信息：

表一

第二步：认识“熵”(entropy)。

信息往往都是比较抽象的，也是难以度量的。如何定量的描述信息作用的大小是计算机实现智能的重要问题。

1948年，香农提出了“信息熵”的概念。一条信息作用大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息，而信息量的度量就等于度量不确定性的多少。熵的单位为bit，我们用以下公式来计算熵的大小:

如果一个随机变量X的可能取值为X={x1,x2,…,xn}，对应的概率为P(X=xi)(i=1,2,…,n)，则随机变量的熵定义为:

例如，大家猜世界杯的冠军，用1至32表示32个足球队，假如什么信息都不知道，则每个队夺冠的概率都一样，即Pi=1/32，i=1，2，…，32；通过上式计算熵可得：

由于我们现在对球队一无所知，我们现在至少需要猜5次才能猜到冠军是谁。比如，首先我先问冠军是否在1至16里面，如果得到肯定，我就继续问是否在1至8里面，如果肯定，我就继续问是否在1至4里面，肯定就继续问1至2，这样5次我便会猜到冠军。如果答案是否定的也是同样的。

但是如果我们知道的信息越多，则确定性就变大，熵就会变小。比如我们知道巴西、法国、阿根廷的实力要强一些，赢球的概率大一些，通过上式所计算的熵就会小一些。反言之，变量的不确定性越大，熵也就越大。

第三步：如何选择和确定节点

这就需要使用决策树归纳算法，决策树归纳算法有几种代表算法，如ID3、C4.5、CART等算法。今天我们主要学习ID3算法，它是在十九世纪70至80年代由J.Ross.Quinlan提出的。ID3算法主要是通过计算某信息作为节点获取的信息，以获得信息量最大的信息作为节点。可通过下式计算：

信息获取量(Information Gain):Gain(A)=Info(D)-Infor_A(D)。

上式就表示用没有A信息时的熵减去有A信息时的熵，得到的差即为以A信息作为节点分类获取了多少信息。以上述实例为例，以年龄为节点计算获取的信息量。

没有年龄信息时，从表一知：共14人，有9人买了套餐，有5人未买套餐，则此时的熵为:

当有年龄信息时，有5个青年人，4个中年人，5个老年人，再分别从这三类中计算买不买套餐的熵：

则以年龄为节点的信息获取量为：

Gain(年龄)=Info(D)-Infor年龄(D)=0.940-0.694=0.246(bits)。

类似的，可计算Gain(收入)=0.029(bits)，Gain(单身)=0.15(bits)，Gain(性别)=0.048(bits)，因为Gain(年龄)最大，所以选择年龄作为第一个根节点。则可以把数据集分为下图：

我们可以看出，中年人已经全部购买就不用再往下分，而青年人和老年人有买和不买，我们再重复信息获取量的步骤，使我们的树不断“生枝发芽”得到最终图一的树。

值得注意以下几点：

一、决策树算法使用同样的过程，递归地形成每个划分上的样本判定树。

递归划分步骤仅当下列条件之一成立停止：

(1)给定结点的所有样本属于同一类，例如上面的中年人，一旦一个属性出现在一个结点上，递归停止。

(2)没有剩余属性可以用来进一步划分样本。在此情况下，使用多数表决。例如上面的年龄、收入、是否单身、性别等信息分类用完后，即将给定的结点转换为树叶结点，并用样本中的多数所在的类标记它。

二、如果数据是连续型的，我们需要将它离散化。比如年龄，我们就需要设置一个阈值，18至39岁为青年，39至60岁为中年，60岁以上为老年。

三、有时候分类过细也不一定是好事情，如果对于一些及其特殊或极端的信息，我们要注意“修枝减叶”，这样我们的模型可能更加符合实际情况。

四、决策树既可以解决分类问题，也可以解决回归问题。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑！