学好全等三角形的技巧(初学全等三角形)

导语：学好全等三角形有诀窍？学霸不用课本，完全靠它

全等三角形是八年级数学的重点和难点，学生通过在综合运用全等三角形性质和全等三角形判定定理的过程中感受到数学与生活息息相关，从而激发学习数学的兴趣。

温故而知新，通过复习全等三角形的性质和判定，培养学生综合应用能力，培养学生的作图及识图能力。这章的主要学习目标是：了解全等形及全等三角形的概念，理解全等三角形的性质.掌握全等三角形的判定，灵活运用全等三角形的判定定理和性质定理，证明简单的全等三角形问题这章的考点有五个。

全等三角形对应边相等，对应角相等不难记住。但在确定对应边和对应角需注意：两个全等三角形的长边与长边，短边与短边分别是对应边，大角与大角，小角与小角分别是对应角.有对顶角的，两个对顶角一定为一对对应角.有公共边的，公共边一定是对应边.有公共角的，公共角一定是对应角。

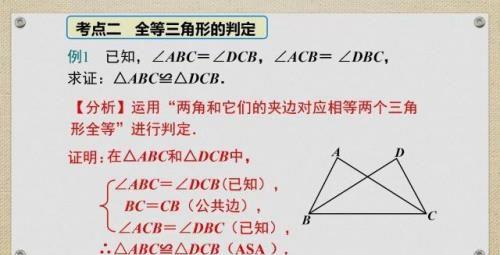
全等三角形的判定是这章的重要内容，首先要清楚证明全等三角形的五个判定：SSS、SAS、AAS、ASA、HL。其次根据已知条件确定使用的判定，再来证明相关条件。特别需要注意的是使用“SAS”这个判定时，角一定要是两边的夹角。

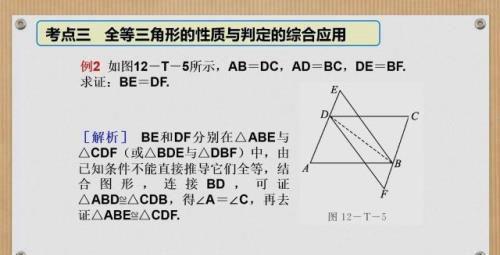
全等三角形的对应边相等和对应角相等，所以在平面几何中，证明两线段相等、两个角相等、两条直线互相平行、两条直线互相垂直等问题时，常常可以通过证明三角形全等来实现.有时在整个证明过程中往往要完成多次三角形全等的证明，才能解决待证（或待求）的问题。

全等三角形广泛应用于现实生活中，为我们解决实际问题提供了有力的工具。把实际问题转化为数学问题，抽象概括出基本的几何图形，并充分利用所学知识构造全等三角形，利用全等三角形可以测量一些不易测量的距离和长度，还可对某些因素作出判断，一般采用以下步骤：（1）先明确实际问题；（2）根据实际抽象出几何图形；（3）经过分析，找出证明途径；（4）书写证明过程。

角的平分线不仅把角分成相等的两部分，而且角的平分线上的点到角两边的距离相等，以及到角两边距离相等的点在这个角的平分线上，这些为我们证明线段（或角）相等提供了便利的方法。应用时要依托全等三角形发挥作用，作辅助线有两种思路，一种作垂线段构造角平分线性质基本图；另一种是构造轴对称图形。

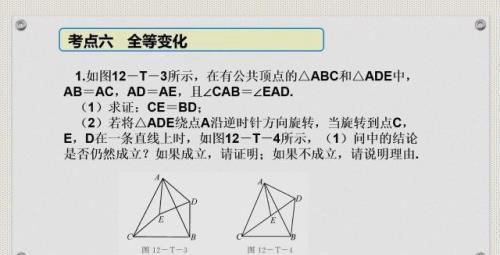
全等变换包括平移变换、翻折变换和旋转变换三种方式.全等变换前后的两个图形全等，具有全等的所有性质，所以利用全等变换是证明线段相等或角相等的基本方法，有时通过全等变换把已知的边（或角）与要证的边（或角）集中在某一个三角形中，便于解决问题。

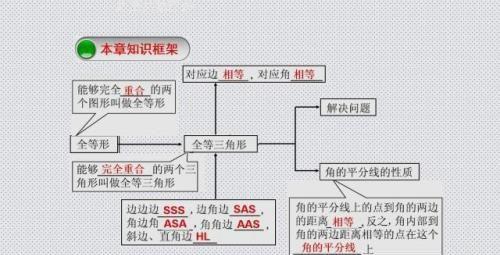
学好全等三角形需要先掌握相关的知识点，再利用知识来解题问题，通过解题再反馈，发现问题、解决问题。最后归纳出体现所学知识的各种题型及解题方法。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小姬创作整理编辑！