突破数学，不止于数学。

全等三角形是初中数学平面几何的重要内容之一，是八年级数学的重点和难点，它为初中解决线段和角相等的问题提供了工具，也为后面平面几何的学习奠定了必要的基础。要学好平面几何，必须重视全等三角形的学习。怎样学好它取得好成绩呢老师为你解答，供八年级同学参考。

1.首先理解“全等”“全等三角形”的含义

首先要搞清楚什么是全等形，能够完全重合的两个图形叫全等形。完全重合有两层含义：

（1）图形的形状相同；

（2）图形的大小相等，两个条件缺一不可。

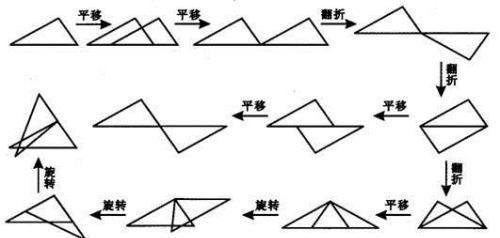
再就是注意组成全等三角形的基本图形大致有一下几种：

（1）平移型 它们可看成有对应边在一直线移动构成的；

（2）翻着型 它们的特征是沿一条直线对折，直线两旁的部分完全重合。

（3）旋转型 它们可以看成是以某一点为中心旋转而成的。

有的题目中可能是两种或三种的复合型，所以心中一定要有这些基本图形，在复杂的图形中分解构造出这些基本图形，证明全等就迎刃而解了。眼中还要看准对应关系，为了不发生差错，在表示三角形全等时，把表示对应顶点的字母写在对应的位置上。

2.熟记全等三角形的性质定理和判定定理

（1）性质定理：全等三角形的对应边相等，对应角相等；全等三角形的对应角的平分线、对应边上的中线、对应边上的高分别相等。性质定理的应用目标性比较明确单一，全等后不是得对应边相等就是得对应角相等。

（2）判定定理（是本章的重点，也是难点）

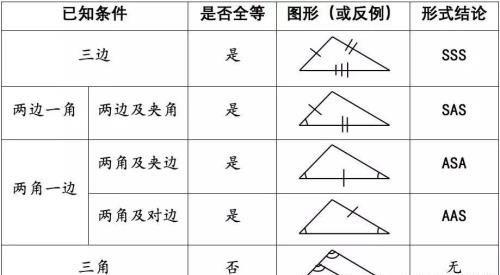
三角形全等判定定理有边边边，边角边，角边角，角角边，斜边直角边。对于一般三角形全等，它们都包含三个元素，并且其中必有一个元素是边。所以证明三角形全等时，必须先找出一条边相等。要注意的是用边边角无法判定两个三角形全等，只有当其中的角已知是直角或钝角才会全等。一定要理解和熟记定理，才能灵活运用。

3.关键点是学会分析全等的思路，灵活运用定理

几何问题的核心就是根据题目中的条件和结论，分析图形，确定已具有的条件和缺少的条件，从已知的其它条件中证明出所需要的条件，从而使问题得以解决。证明三角形全等常用的方法有综合法和分析法。综合法就是从题目的条件出发，进行一步步推理证明，最后达到待证的结论。

要善于发现和利用隐含的条件，比如：公共边，公共角，对顶角等。找边相等时，中点，中线，等腰三角形，平行四边形等都能得到边相等；找角相等时，同角的余角或补角，角平分线，等腰三角形，多个垂直（利用互余）等都能得到角相等。这些都是证明全等的依据。分析法就是从题目的结论出发，分析要想得到这个结论需要什么条件，再结合题目中给的条件和隐含条件，就能找到全等三角形，问题就可以解决。推理的过程要做到有理有据，条理清楚，层次分明，表达准确。

不同的条件，有不同思路：

例如：已知两边的情况下：(1)找夹角利用SAS(2)找第三边利SSS(3)找直角利用 HI；

已知两角的情况下：找任意边利用ASA或AAS；

已知一边一角的情况下：(1)当边是角的对边时，找任一角AAS (2)当边是角的邻边时，找这条边的另一边ASA或找这条边的对角AA或找该角的另一边SAS

4.三角形全等是证明线段相等、角相等的重要途径

“证相等，找全等”，全等三角形性质的基本应用，就是证明两个角相等或两条线段相等，进而间接证明出两直线平行或垂直或两线段的和等于一条线段。

注重典型例题的收集整理

不要只是盲目的做题，一定要注重把有代表性的题目整理在一起进行对比，发现题目之间差异与联系，从而发现其中之间的技巧、方法，总结出规律，以便于今后的应用。并且把一些有代表性的不同题型与全等三角形的基本结构图形去对照，你会发现都有规律可循。

还有就是要充分利用好改错本，对平时或考试做错以及不会做的题目，及时改做在错题本上，把错误的地方和正确的答案，都要写清楚，以便加以对照、鉴别，在不断比较鉴别中，才会有进步，才会取得优异成绩。

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小苹创作整理编辑！