导语：「高中数学」利用单调性求函数最值，及结合最值求解参数的范围∽

函数的最值问题，一般跟函数的单调性，不等式等结合在一起考查。

1、求已知函数的最值.

注:求分段函数的最值，可以画出图像观察；也可以求出每一段函数的值域，进而得出最值.

注:将解析式进行转化，使其只有分母上含有x，从而根据x的范围逐步求出值域.

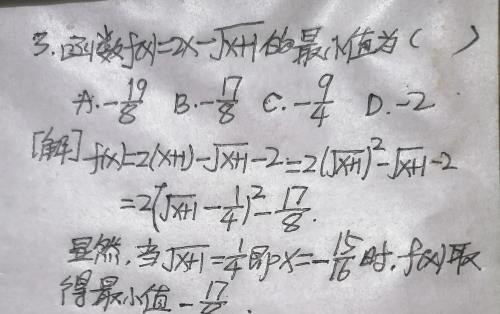
注:将根式√(x+1)看做一个整体(可设为t，t≥0)，进行配方，利用二次函数的性质得出最小值.

注:解三个不等式组，可得出分段函数f(x)的解析式，分别求出每段函数的值域，其并集就是整个f(x)的值域.

注:f(x)每一段的“定义域”需要求出来，进而可画出图像得出f(x)的值域.

2、求含参数的二次函数的最值，及求参数的取值范围

(1)解法:首先将二次函数化为y=a(x-h)+k的形式，再确定抛物线的开口方向、对称轴及顶点，根据x的定义区间结合大致图像确定最大值或最小值。

(2)含参数的二次函数的最值问题，主要有几种类型:

①区间固定，对称轴变动(含参数)，求最值；

②对称轴固定，区间变动(含参数)，求最值；

③区间固定，最值也固定，对称轴变动，求参数的取值范围.

求解时，通常根据区间端点和对称轴的相对位置进行分类讨论.

注:二次函数f(x)在一个开区间上没有最大值和最小值，说明这个开区间在对称轴的左侧或右侧，因为是开区间，故端点可以在对称轴上，反正取不到这一点的函数值.

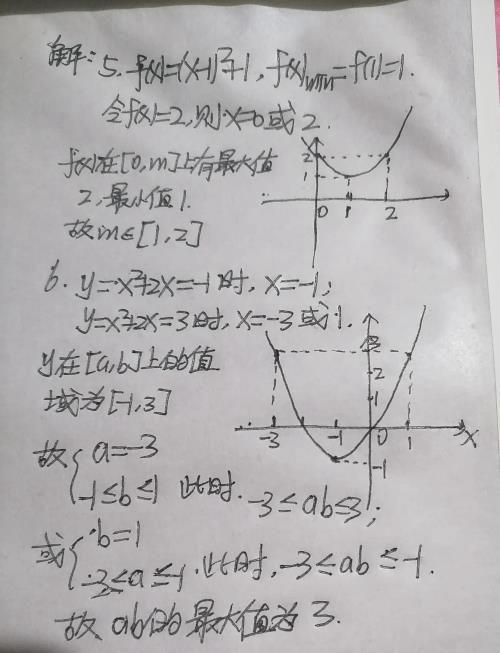
注:上面3道题是同一类型，画出图像，标出对称轴，标出最大值和最小值及对应的x值，观察x的区间.

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小芦创作整理编辑！