如何证明一个三角形为等边三角形(求证三角形是等边三角形)

导语：初中几何题-证明一个三角形是等边三角形

初中几何题-证明一个三角形是等边三角形

在图中， C在BD上， 此外三角形ABC和三角形ECD是等边三角形， 如果M是BE的中点， N是AD的中点，证明三角形MNC是等边三角形。

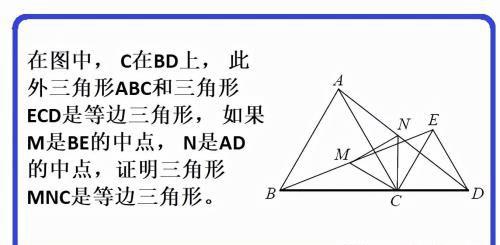
证明：方法1-初中的几何法

因为三角形ABC是等边的， 所以BC=AC

因为三角形ECD是等边的，所以CE=CD，

由于BCD是一条直线所以，∠BCE=180°-60°=120°

同理∠ACD=180°-120°=60°

所以△BCE全等于△ACD，（边角边定理）

因此∠CAN=∠CBM

BE=AD，

另外N是BE的中点， N是AD的中点，因此BM=AE/2, AN=AD/2

因此有BM=CN

利用上面证明的∠CAN=∠CBM

以及AC=BC，可以证出：

三角形ANC全等于三角形BMC，（边角边定理）

因此

CM = CN.

∠MCB=∠NCA

由于∠ECD = 60°=∠MCB+∠MCA

=∠NCA+∠MCA

=∠MCN

∠MCN = 60°

结合前面已经证明的BM=CN

因此证明出三角形MNC是等边三角形。

证明2： 高中的解析几何方法，如图建立各点坐标,

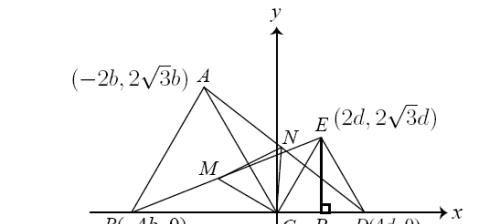
然后M和N点的坐标就确定了。

分别计算MN， MC和NC的两点之间的距离平方，即可证得，

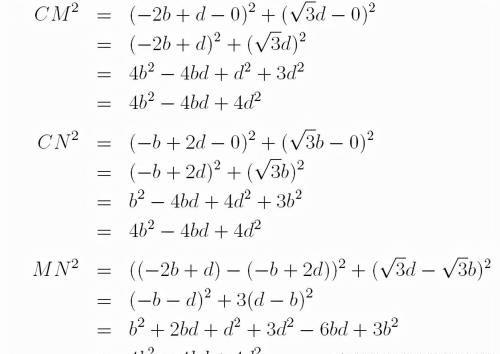
免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小德创作整理编辑！