组合图形面积计算方法(组合图形面积计算题)

导语：组合图形面积计算

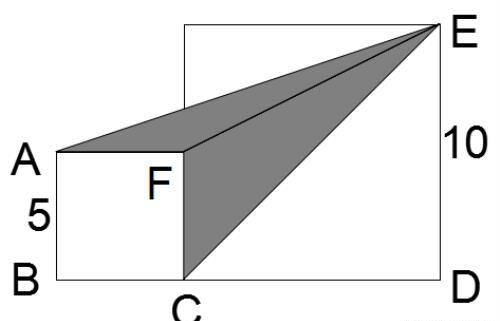
例1 下图，大正方形的边长是10厘米，小正方形的边长是5厘米。问阴影部分的面积是多少平方厘米？

解析：本题方法较多：

方法一：△AFE的面积+△CFE的面积，二者的底和高均可以明显看出；

方法二：用梯形ABDE的面积减空白也可，阴影面积是37.5平方厘米

例2 图中两个正方形的边长分别是6厘米和4厘米，求阴影部分的面积。

解析：连接CB，如下图，利用梯形上下底平行，可得下图阴影部分面积相等，所以题中阴影占大正方形面积一半。故答案是18平方厘米。

例3 下图中，AD=8厘米，EC=5厘米，求阴影部分的面积

解析：如下补全图形为长方形，可得两块阴影部分面积相等，故答案是5×8=40（平方厘米）

例4 求下图中阴影部分的面积。（单位：厘米）

解析：按照一般方法，本题应该用两个小半圆的面积和加上直角三角形面积，再减去大半圆面积。结果是96平方厘米，会发现阴影面积恰好是直角三角形面积。其实下图两块“月牙”阴影面积和直角三角形是相等的。可以记住该结论。

例5 如图中，AD = 3 厘米，BC = 7 厘米，∠A =∠B = 90°，求四边形 ADBC 的面积。

解析：把该四边形补成一个等腰直角三角形，如下图，用加减法计算即可。答案是20平方厘米

例6 两个大小不同的等腰直角三角形放置如图（单位：cm），求重合部分的面积。

解析：其实图中所有三角形都为等腰直角三角形，本题方法特别多，比如可以用△ACG面积-△ADE的面积，结果是17平方厘米.

例7 求如图中阴影部分的面积。（单位：厘米）

解析：图中AB空白为正方形面积与圆面积差的一半，中间空白为两个扇形与正方形的差，可得结果是129平方厘米。

例8 如图中 O 为小圆的圆心，C 为大圆的圆心，CO 垂直于 AB ，三角形 ABC 的面积是 45 平方厘米。阴影部分的面积是多少平方厘米？

解析：如下图，两块阴影面积相等，其证明方法是让二者都加上中间的空白弓形后可证相等。故结果是45平方厘米。

练习

1.如图，四边形 ABCD 被分为四块，其中三块的面积分别为 4、6、12 平方厘米，求三角形 DEC 的面积是多少。（答案：8平方厘米）

2.如图中，正方形的边长是 10 厘米，求图中阴影部分的面积。（答案：57平方厘米）

3.如图中正方形的面积是 100 平方厘米，内半圆的面积是外半圆面积的四分之一，求阴影部分的面积是多少平方厘米？（答案：80.375平方厘米）

4.如图，三条边分别是 6 厘米、8 厘米、10 厘米的直角三角形，将它的直角边对折到斜边上去，与斜边重合，则图中阴影部分（即未被盖住的部分）的面积是多少平方厘米？（答案：6平方厘米，本题要用勾股定理）

5.如下图，平行四边形 ABCD 的周长是 90厘米，以 BC 为底的高 AE 是 14 厘米，以 CD 为底的高AF 是 16 厘米。求平行四边形的面积。（答案：336平方厘米）

本文内容由小余整理编辑！