> 科技
高考数学圆的方程(圆的方程在高考中的地位)
导语:高考考纲与考向分析——圆的方程
(1)掌握确定圆的几何要素,掌握圆的标准方程与一般方程.
(2)能用圆的方程解决一些简单的问题.
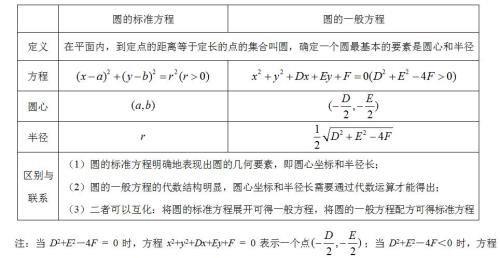
知识点详解一、圆的方程
二、点与圆的位置关系
三、必记结论
(1)圆的三个性质
①圆心在过切点且垂直于切线的直线上;
②圆心在任一弦的中垂线上;
③两圆相切时,切点与两圆心三点共线.
(2)两个圆系方程
具有某些共同性质的圆的集合称为圆系,它们的方程叫圆系方程.
考向分析考向一 求圆的方程
1.求圆的方程必须具备三个独立的条件.从圆的标准方程来看,关键在于求出圆心坐标和半径,从圆的一般方程来讲,能知道圆上的三个点即可求出圆的方程,因此,待定系数法是求圆的方程常用的方法.
2.用几何法求圆的方程,要充分运用圆的几何性质,如“圆心在圆的任一条弦的垂直平分线上”,“半径、弦心距、弦长的一半构成直角三角形”.
考向二 与圆有关的对称问题
1.圆的轴对称性:圆关于直径所在的直线对称.
2.圆关于点对称:
(1)求已知圆关于某点对称的圆,只需确定所求圆的圆心位置;
(2)两圆关于点对称,则此点为两圆圆心连线的中点.
3.圆关于直线对称:
(1)求已知圆关于某条直线对称的圆,只需确定所求圆的圆心位置;
(2)两圆关于直线对称,则此直线为两圆圆心连线的垂直平分线.
考向三 与圆有关的轨迹问题
考向四 与圆有关的最值问题
对于圆中的最值问题,一般是根据条件列出关于所求目标的式子——函数关系式,然后根据函数关系式的特征选用参数法、配方法、判别式法等,应用不等式的性质求出最值.特别地,要利用圆的几何性质,根据式子的几何意义求解,这正是数形结合思想的应用.
【名师点睛】
本文内容由小涵整理编辑!