四种方法解高次方程后一种方法才是绝杀的方法(高次方程的解法公式)

导语：四种方法解高次方程，最后一种方法才是绝杀

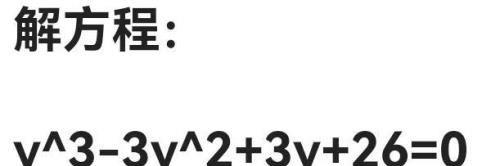
解方程：

y^3-3y^2+3y+26=0

解法①：原方程可变为

（y^3+8）-3y（y+2）+9y+18=0

（y+2）（y^2-2y+4）-3y（y+2）+9（y+2）=0

（y+2）（y^2-2y+4-3y+9）=0

（y+2）（y^2-5y+13）=0

∴y=-2

解法②：特殊值试根+长除法

通过试根y=-2是原方程的解：

（y+2）（y^2-5y+13）

y^3-3y^2+3y+26

y^3+2y^2

-5y^2+3y

-5y^2-10y

13y+26

13y+26

0

解法③：

原方程可变为：（y^3-2y^2+y）-y^2+2y+26=0

y（y-1）^2-（y^2-2y+1）+27=0

y（y-1）^2-（y-1）^2+27=0

（y-1）^3=-27

（y-1）^3=-3^3

y-1=-3

y=-2

解法④：快速解法

∵（y-1）^3=y^3-3y^2+3y-1

∴原方程可变为：（y-1）^3+1+26=0

∴（y-1）^3=-3^3

∴y-1=-3

∴y=-2

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小奈创作整理编辑！