关于分式方程无解的探讨和反思(关于分式方程无解的探讨和反思作文)

通过对近几年中考数学题的分析可以发现，在中考中频繁出现考查分式方程无解的题型.然而很多学生在碰到无解的题型时往往会有些自我怀疑，担心分式方程无解是由于解题过程不正确导致的，会重复计算，这将会浪费大量的时间和精力.如果我们在实际解题中能够正确地应用分式方程无解的性质，有助于有效提高我们的解题效率，更加清晰地认识题目，从而解决其他的问题.因此，下面我们将借助几道例题对分式方程无解题型进行详细的分析和探讨.

一、分式方程无解的含义

分式方程无解是指无论取何值都不能满足分式方程等号两边相等，分式方程无解主要有两种情形：一是原分式方程在等号两边同时乘最简公分母化简为等式方程后，等式方程无解；第二种情形是在分式方程化为等式方程后，整式方程有解，但是这个解却让原来的分式方程分母为0，这个解就叫作分式方程的增根.

二、例题分析

例1 解方程

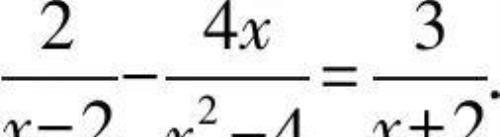
解 在分式方程两边同时乘(x+2)(x-2)，

得2(x+2)-4x=3(x-2).

根据题意解这个方程，得x=2.

x=2代入原方程可知，当x=2时，原分式方程的分母为0，此时分式方程没有意义，因此，x=2是原分式方程的增根.没有数值使原分式方程的成立，因此，原方程无解.

分析 首先我们对原分式方程进行观察，由于分母不能为0，因此，可以直接看出分式方程中未知数的取值范围为x≠2且x≠-2，但是在对原分式方程化为整式方程时，未知数的取值范围有所扩大，可以取全体实数，然而整式方程未知数定义域下所求出的值恰好不满足原分式方程定义域，使得分母为0，此时所求出的未知数的值就是原方程的增根，故原方程无解.

例2 解方程

解 首先对分式方程进行整理，两边同时乘最简公分母(x+2)，得x-1=3-x+2(2+x).

整理等式可得：0x=8.

因为这个整式方程无解，所以原分式方程也无解.

分析 这种分式方程在转化成整式方程后，整式方程无解，那么原分式方程肯定同样无解，所以方程无解和有增根是两个不同的概念，分式方程无解并不一定有增根产生.

例3 如果方程

无解，那么m=________.

解 原方程

将分式方程转化为整式方程，等号两边同时乘(x-2)，

得x-3=-m.

解等式x=3-m.

由于题目提到原方程无解，所以这个解应该是原分式方程的增根.即x=2，也就是2=3-m，

解得m=1.

因此，当m=1时，原分式方程无解.

分析 因为此题是将分式方程转成一元一次方程，但是这个一元一次方程只有一个根，所以说如果这个根是原分式方程的增根，那么原分式方程无解.但是我们要注意分式方程有增根并不代表一定无解，随着我们学习内容的进一步深入，会理解其中的原理.

例4 当a为何值时，关于x的方程

会产生增根

解 让分式方程两边同时乘(x+2)(x-2)，

得2(x+2)+ax=3(x-2).

整理得(a-1)x=-10.

如果原分式方程有增根，那么x=2或-2是方程①的根.

将x=2或者-2代入方程①中，

可以解得，a=-4或6.

分析 在解答这类题时首先要将分式方程转化成整式方程，然后解整式方程，并满足原来的分式方程分母为零的数值，这个数则是原分式方程的增根.将增根代入转化后的整式方程，然后将原来方程中含字母的值求出来.

如果将此题中的“会产生增根”改为“无解”，这时候还要考虑转化后的整式方程(a-1)x=-10本身无解的情况，具体解法如下：

解 方程两边都乘(x+2)(x-2)，

得2(x+2)+ax=3(x-2).

整理得(a-1)x=-10.

如果原来的分式方程无解，那么有两种情况：

(1)当a-1=0，也就是a=1时，方程②为0x=-10；

(2)假设方程②的解正好是原来的分式方程的增根，那么原来的分式方程没有解.如果原分式方程有增根，增根为x=2或-2，把x=2或-2代入方程②中，可以得到a=-4或6.

综上所述，a=1或a=-4或a=6时，原分式方程无解.

三、结束语

总之，原分式方程无解这种题型在中考时经常考查，需要我们认真总结和分析分式方程无解的情形，掌握分式方程无解和分式方程有增根的含义与区别.解分式方程有增根即解转化后的分式方程的值满足原分式方程分母为0，分式方程无解则有原分式方程无解和转化后的整式方程无解两种情况，包含有增根的情况，需要具体问题具体分析.同时也要认真总结，针对不同题型采用不同方法，匡正解题思路.

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑！