数学层次(数学中的几层什么意思)
导语:谈谈数学中的层:层化
话题:
小石头/编
我们已经知道,
只有 当 预层 同时 满足 单一性 和 粘合性 时,才被称为 层;也就是说,并不是所有的预层都是层 。不过,虽然如此,但是我们却可以从任何预层构造一个层,这就是本篇要给大家介绍的内容——层化(sheafification)。
——§ 起 §——
回忆 前文 的 例子 №1:
设 X 和 E 都是 拓扑空间,则 可以构造一个 层 Cᴱ,
将 X 中的任意开集 U 映射为 全体 U 到 E 的 连续映射,即, Cᴱ(U) = C(U, E);将 X 中的 任意开集对 V ⊆ U 映射为限制映射 rᴜᴠ : Cᴱ(U) → Cᴱ(V), s ↦ s|ᴠ(注:关于 Cᴱ 是层 很容易验证,大家不妨自己试一试。)
现在 让我们 对 №1 进行改造:
首先,引入 一个 从 E 到 X 的 连续映射 p: E → X,我们要求 p 局部同胚(local homeomorphism),即,
对于每一个 e ∈ E,都存在 开集 N ∋ e, U ∋ p(e) 使得 p|ɴ: N → U 同胚;然后,通过 p 对于 每个 C(U, E) 中的映射 进行筛选,定义:
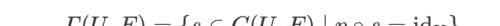
即,使得下图交换,
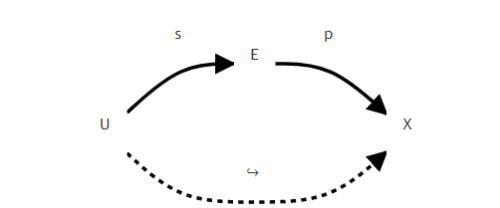
接着,仿照 №1,可构造一个新的 层 ΓE,如下:
ΓE(U) = Γ(U, E);rᴜᴠ : ΓE(U) → ΓE(V), s ↦ s|ᴠ;最后,可 验证 ΓE 的确是层,验证 过程与上面的 Cᴱ 类似,这里就不再累述了。
至此,就通过 E 和 p: E → X 构造了一个 X 上的 层,我们将 E 和 p 放在一起,称为 X 上的一个 层空间 (sheaf space),记为 (E, p)。
——§ 承 §——
疑问:看到这里的朋友,可能对于 层空间 定义 中 p 是 局部同胚的 条件 感到突兀。没关系,耐心 往后看 大家就会明白,为什么要引入 这个 条件了。
这里先抛开原因不说,我们需要知道的是,该条件的引入 可以使 ΓE 具有 很多良好的性质,下面来看一看:
首先,设 V 是 E 中的任意开集 ,对任意 x ∈ p(V) 取 e ∈ V, p(e) = x, 由于 p 是局部同胚,存在 开集 N ∋ e 使 p|ɴ 是同胚,并 将 e 在 N 中的开邻域 V ∩ N 映射为 x 在 p(V) 中的开邻域 p(V ∩ N),于是 任意 x ∈ p(V) 都是 p(V) 的内点,进而 p(V) 是开集,这说明,p 是一个 开映射。
其次,设 U 是 X 中的任意开集,s ∈ ΓE(U),对于任意 e ∈ s(U),由于 p 是局部同胚,存在 开集 N ∋ e 使 p|ɴ 是同胚,于是 p|ɴ⁻¹ 将 开集 p(N) ∩ U 映射为 e 在 s(U) 中的开邻域 N ∩ s(U), 所以 任意 e ∈ s(U) 都是 s(U) 的内点,进而 s(U) 是开集,故,s 也是 开映射。
再次,将 上面 全体 s(U) 这样的开集 记为 ℬ,对于 任意 e ∈ E,以及 e 的任意开邻域 W, 由于 p 是局部同胚,存在 开集 N ∋ e 使 p|ɴ 是同胚,于是 p|ɴ(N ∩ W) 是 开集,故 s(p|ɴ(N ∩ W)) ∈ ℬ,而且有,
p|ɴ(s(p|ɴ(N ∩ W))) = id(p|ɴ(N ∩ W)) = p|ɴ(N ∩ W) ⇒ s(p|ɴ(N ∩ W)) = N ∩ W
于是, e ∈ s(p|ɴ(N ∩ W)) ⊆ W,故 ℬ 是 E 的一个拓扑基。
最后,给定 x ∈ X,考虑 p⁻¹(x)。对于任意 s ∈ ΓE(U)open U ∋ x,由,
p(s(x)) = idᴜ(x) = x
有,
s(x) ∈ p⁻¹(p(s(x))) = p⁻¹(x)
故,对 每个开集 U ∋ x,可定义映射,
σᴜ: ΓE(U) → p⁻¹(x),s ↦ s(x)
其对 前序关系 U ⊇ V ∋ x,有,
σᴠ(rᴜᴠ(s)) = rᴜᴠ(s)(x) = s|ᴠ(x) = s(x) = σᴜ(s)
即,
σᴠ ∘ rᴜᴠ = σᴜ
这说明,p⁻¹(x), (σᴜ)U ∋ x 是 (以 X 中全体包括 x 的开集为方向集的 ΓE 中正向系 的)一个目标,我们 断言 这个目标 就是 层 ΓE 在 x 处的茎,即,
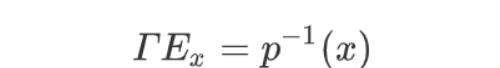
为此,需要证明 该目标 是 一个 正向极限,证:有,
对于任意 e ∈ p⁻¹(x),因为 p 局部同胚,故存在 e 的开领域 N 使得 p|ɴ : N → U 是同构,其中 U 是 X 中的开集,显然 p|ɴ⁻¹ ∈ Γ(U, E) = ΓE(U),于是有 σᴜ(p|ɴ⁻¹) = p|ɴ⁻¹(x) = e,即,e ∈ Im(σᴜ);对于 任意 s ∈ ΓE(U), t ∈ ΓE(V),根据上面结论,知 W = s(U) ∩ t(V) 是 E 中开集,以及 p(W) ⊆ U, V 是 X 中开集,考虑到 x ∈ X 其实是任意的,于是有,σᴜ(s) = σᴠ(t) ⇒ s(x) = t(x) ⇒ s|p(W)(x) = t|p(W)(x) ⇒ rᴜ,p(W)(s) = rᴠ,p(W)(t) ∈ ΓE(p(W))注:实际上 s|p(W) = p|ᴡ⁻¹ = t|p(W)
综上,根据正向极限判定定理,知 p⁻¹(x), (σᴜ)U ∋ x 是正向极限。▉
从上面的证明过程,还可以看出: p⁻¹(x) 是 E 的 离散子空间,因为:有 N ∩ p⁻¹(x) = {e} 是 p⁻¹(x) 的 开集。
——§ 转 §——
再回来,本篇的最终目的是从 X 上的 预层 F 构造一个 层,现在以及可以 从 层空间 构造 层 了,于是只需要 从 F 构造出 一个 层空间,就大功告成了!
首先,我们已经知道,对于任意 x ∈ X 都 可以构造出 一个 茎 F᙮, 于是 考虑 F 的全体 茎的 无交并,
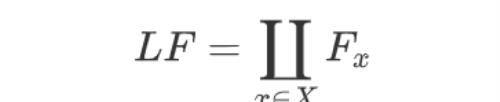
这里自然存在一个映射,
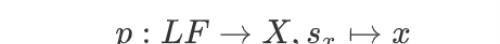
也就是 p⁻¹(x) = F᙮ 。
然后,对于每个 X 的开集 U 以及每个 s ∈ F(U),都可以定义映射,
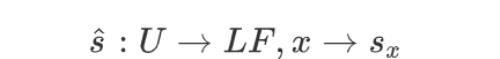
若规定,
每个 sˆ(U) = {s᙮ ∈ F᙮ | x ∈ U} 都是开集;我们则断言,所有 这些开集 组成 LF 的一个拓扑基,因为:
显然 这些开集 是 LF 的一个 覆盖;对于 每个 e ∈ sˆ(U) ∩ tˆ(V) , (s ∈ F(U), t ∈ F(V) ) ,有 s᙮=t᙮, x = p(e),于是,根据 茎的性质,存在 x 的开邻域 W ⊆ U ∩ V 使得 rᴜᴡ(s) = rᴠᴡ(t),进而,(rᴜᴡ(s))ˆ(W) = (rᴠᴡ(t))ˆ(W) 就是 e 在 sˆ(U) ∩ tˆ(V) 中的开邻域;这样,这些开集 就满足了 拓扑基的定义。
于是,我们在 LF 中赋予 该拓扑基生成的拓扑, LF 就成为一个拓扑空间。
接着,由于,对于任意开集 U ⊆ X,有,

于是 f⁻¹(U) 是开集(开集的并是开集),进而 p是连续的。
最后,考虑 p 在 任意 开集 sˆ(U) 上的限制 p| sˆ(U),其继承 p 的连续性,同时其逆为,
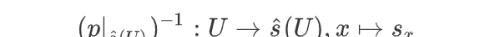
这其实就是 sˆ 将陪域限制为其值域的结果,故其逆是满射,又因为:
对于 任意 x ≠ y ∈ X,由于 LF 中 F᙮ 与 Fy 是无交的,所以 s᙮ ≠ sy(在 LF 中),因此 sˆ 是单射;对于任意 s᙮ ∈ sˆ(U), (x ∈ U) 的任意 开邻域 N, 总存在 拓扑基 V = sˆ(W) ∋ s᙮ 使得 V ⊆ N,而 sˆ⁻¹(V) = W (sˆ 是单射)是 x 的 开邻域,于是 sˆ 连续的;所以 其逆是 连续的双射,于是 p| sˆ(U) 一个 同胚,即 p 是局部同胚。
至此,我就从 X 上的预层 F 构成出来 一个 X 上的 层空间 (LF, p),进而,就可以再 从 (LF, p) 构造出 层 ΓLF 来了,我们称 整个过程为 预层 F 的层化(sheafification)。
还记得 前面那个 疑问 吗? 实际上,层空间 是层化过程中的中间产物,在层化过程中 p 自然就是 局部同胚的,因此 这个条件 自然就被引入了 层空间的 定义。
——§ 合 §——
总结,设 F 是 拓扑空间 X 上的 预层,则 通过 以上 两个步骤,即:
第一步:先由 F 构造一个与 X 有关联的 拓扑空间 LF,这里的关联是指,存在 一个 从 LF 到 X 的 局部同胚的 连续映射 p: LF → X,它们组成 X 上的 一个 层空间 (LF, p);第二步:然后再从 层空间 (LF, p) 构造 出 一个层 ΓLF可将 F 层化 为 一个 层 ΓLF。
这个层化出来的 层,不仅 具有 前面 提到的 良好性质(由于 p 自然 就有 局部同胚性),而且 通过 进一步 分析 层(预层、层空间) 之间的关系,我们 可以 证明:
层化出的 层 ΓLF 是从 F 出发所能创造出的 层中 “最好” 的 那个;这将是我们的 下一篇 的核心内容。
最后,需要说明:以上 构造过程 是 集合的预层 的层化,对于 Abel群的预层 的层化,小石头将在后续文章中详细介绍。
附录:
拓扑空间之间的映射 f : X→Y,若将 开集 映射回 开集,即,
∀ V ⊆ Y 是开集 ⇒ f⁻¹(V) 是开集则称 f 是连续的(等价定义:对于任意 x∈X,总存在 f(x) 的邻域 V,使得 f⁻¹(V) 是 x 的邻域)。
反过来,若将 开集映射到开集,即,
∀ U ⊆ X 是开集 ⇒ f(U) 是开集则称 f 是开的。一个 既连续又开的 双射(也就是 f 和 f⁻¹ 都是 连续的 或 开的 双射),称为 同胚。
非空集合 X 的 一个子集族 ℬ,如果满足:
ℬ 覆盖 X;对于 任意 U, V ∈ ℬ 以及 任意 x ∈U ∩ V,都存在 W ∈ ℬ 使得 x ∈ W ⊆ U ∩ V;则称 ℬ 是 集合 X 的 拓扑基。通过 拓扑基 可以生成如下拓扑结构:
τ = { W | ∃ ℛ ⊆ ℬ, W = ∪ℛ };使得 X 升级为 一个拓扑空间。
反过来,若 X 本来就是拓扑空间,而 ℬ 刚好生成了 X 的 拓扑结构,此时 称 ℬ 是 拓扑空间 X 的 一个拓扑基,有定理:
ℬ 是 拓扑空间 X 的一个 拓扑基,当且仅当,对于任意 x ∈ X 的任意 领域 N,都存在 W ∈ ℬ 使得 x ∈ W ⊆ N;(层化中的证明需要 一些 《拓扑学》知识,小石头将其放在 附录里面,当以这里仅仅只是引用,更详细的知识大家可参考相关教材。)
(下一篇 我们 讨论 层间关系 —— 层态射,态射概念的 引入 标志着 我们的讨论 将要 进入 范畴论 阶段,对 《范畴论》 有兴趣的朋友,敬请期待!)
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小涵创作整理编辑!