用配平方法解方程(配平方程式原则)

导语：配和的平方等于零不行，构造法解方程

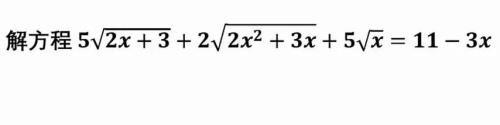
x>0

解法①:原方程变为:

5[√（2x+3）+√x]+2.√（2x+3）.√x+3x-11=0

∴（2x+3）+x+5[√（2x+3）+√x]+2√（2x+3）√x-14=0

∴[√（2x+3）+√x]²+5[√（2x+3）+√x]-14=0

∴[√（2x+3）+√x+7][√（2x+3）+√x-2]=0

∵√（2x+3）+√x+7≠0

∴只存在√（2x+3）+√x-2=0

∴2x+3=4+x-4√x

∴4√x=1-x（0<x<1）

∴16x=x²-2x+1

∴x²-18x+1=0

∴x=9+4√5（∵0<x<1，舍去）或x=9-4√5

∴经验根，原方程的解为:x=9-4√5

解法②：原方程变为:

5√（2x+3）+2√x.√（2x+3）+5√x=-（2x+3）-x+14

令√（2x+3）=a（a≥0），√x=b（b>0）

∴5a+2ab+5b=14-a²-b²

（a+b）²+5（a+b）-14=0

∴（a+b+7）（a+b-2）=0

∴a+b=-7（∵a+b>0，∴舍去）或a+b=2

∴√（2x+3）+√x=2

∴√（2x+3）=2-√x

∴2x+3=4+x-4√x

∴4√x=1-x（0<x<1）

∴16x=x²-2x+1

∴x²-18x+1=0

∴x=9+4√5（舍去）或x=9-4√5

∴经验根，原方程的解为:x=9-4√5

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小迪创作整理编辑！