高中数学函数的综合性质考点有哪些(高中数学函数综合题)

导语：高中数学函数的综合性质考点

高中数学研究的是数与数，数与几何，数形，形数之间的"爱恨情仇"关系，今天我们来看高考高频考点，函数的性质(奇偶性，单调性，周期性等)，以下是近几年理科高考题型，难度不大，一起来分析。

对于正余弦函数性质①对称中心与零点的联系②对称轴与最值点联系③最值点与零点之间距离与周期关系④单调与周期的关系，具体解析如下:

此题考查抽象函数奇函数的单调性质，对于奇函数来说关于原点对称图像相同单调要满足奇函数在某区间单调递减只需f(x1)≤f(x)≤f(x2)(其中x1＝－x2)则x2≤x≤x1故此题f(1)≤f(x)≤f(－1)具体解法参考以下:

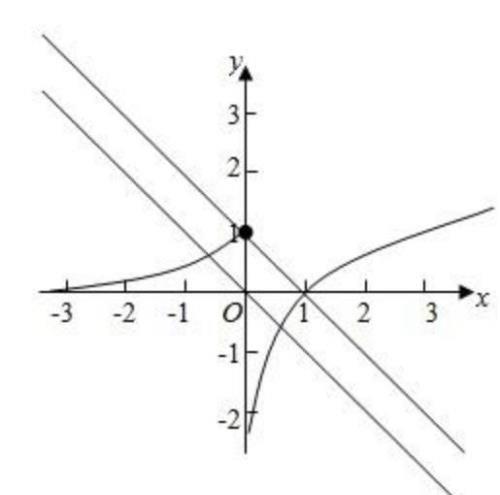
此题考查函数的零点问题，解零点问题，常见的数形结合，根据题设令g(x)＝0,f(x)＝－x－a,分别画出分段函数f(x)的图像且f(x)＝－x(x在(－∞,∞)范围)的图像如下:平移f(x)＝－x(在与分段函数图像都相交范围内)当截距越大说明a越小故在交点(0,1)处取得最小值－1,由图可知-1≤a,所以a的取值范围是[－1,∞].正确答案选C

解析此题看查函数的奇偶性，单调性，零点，最大最小值

①判断函数奇偶性，首先定义域要关于原点对称，显然条件符合，再用奇偶定义判断是否奇偶函数，此函数满足f(x)＝f(－x),f(x)＋f(－x)≠0.故是偶函数

②f(x)在区间(π/2,π)上单调性，f(x)＝sinx＋sinx＝2sinx在区间(π/2,π)上单调递减，故命题不对现在可以排除A,D不是此题答案

③根据区间(－π,0],f(x)＝－sinx－sinx＝－2sinx＝0得x＝－π或者0.在区间(0,π]上时，f(x)＝2sinx＝0得x＝π.故f(x)在区间［－π,π］上有3个零点。画出函数图像可直观看出。③不对,正确答案选C

④由③画出一个周期内的图像可知道0≤f(x)≤2④正确

总结：熟悉各函数的周期性，单调性，奇偶性，对称性等性质(尤其是三角函数高考频率高)，当然其他函数也要熟悉，数形结合，分类讨论即可

欢迎大家一起讨论，不当之处欢迎指出。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小信创作整理编辑！