为什么正弦和余弦曲线构成波形不一样(正弦曲线和余弦曲线统称)

导语：为什么正弦和余弦曲线构成波形？

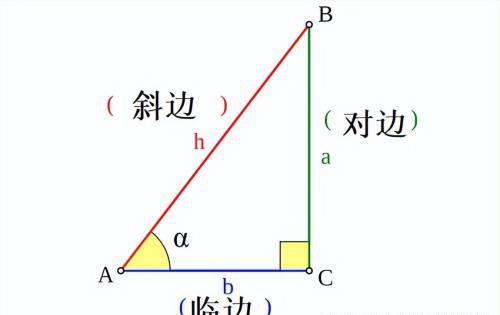
想象一个直角三角形。然后你可能会记得，你可以用正弦和余弦函数来了解更多关于三角形的知识。如果其中一个角α不是直角，那么就有

sinα=对边/斜边

以及

cosα=临边/斜边

正弦和余弦函数能做的远不止帮助你解决几何问题。它们可以用来构建任何波形——你正在听的音乐，你通过wifi发送的数字信号，甚至是海上的波浪——无论这些自然或人为的振荡有多复杂。

循环往复

构造波的第一步是想象在笛卡尔坐标中画一个半径为1的圆，圆心位于点（0,0）处。想象从最右边的点（1,0）开始，沿逆时针方向绕圆运动。当你旋转了一个小于90度的α角(对应于小于π/2弧度)，你所处的点定义了一个直角三角形，这个三角形的斜边长度为1，因为这个点位于半径为1的圆上。对于这个三角形我们有:

cosα=x,

sinα=y

单位圆上的一个点构成的直角三角形

你可以继续反时针旋转使得角α大于π/2, 这时候直角三角形有三个顶点（0,0）， （x,0）和（x,y）, 因此不再受α的约束。

然而，没有什么可以阻止你扩展正弦和余弦的定义，与我们之前的类比:

cosα=x,

sinα=y,

这里的(x, y)就是你现在所在的点。

当你绕着圆移动一圈时正弦和余弦会发生什么变化?在圆周的一圈中，你将转一个2π角。当你绕着圆移动时，你的纵坐标(正弦值)开始于0并稳定增加，直到你在圆顶部时达到最大值1。当你继续转动时，它又以对称的方式下降到0，在达到最小值-1之前，最后又回到0。

如果你画出纵坐标(下图中红色部分)随角度(从0到2π)的变化，你会得到一个规则的波形状。它从0开始，上升到最大值1，然后再次下降到0，然后下降到最小值-1，然后再次上升到0。

当你转动第二圈时，这种波动模式会重复，增加你从2π到4π的角度，第三圈从4π到6π的角度，以此类推。你会得到一个无限长的，完全规则的波。水平坐标(余弦)给出了一个类似的完美波(上面用蓝色标出)，沿着水平轴与第一个波偏移了一段距离。这将正弦和余弦的定义扩展到大于π/2。(你也可以通过顺时针绕圈来定义负数的正弦和余弦。)

挤压和拉伸

我们已经知道绕单位圆运动可以得到两个函数，正弦函数和余弦函数，每个函数都有一个描述规则波的图形。当你在教科书中遇到这些函数时，变量通常被称为x而不是α，所以你会看到类似的东西

F(x)=sin(x)

G(x)=cos(x)

我们现在转换到这个符号。这意味着它现在表示的是以前的角度它不再表示单位圆上一点的坐标。这可能有点令人困惑，但坚持下去，你会习惯的。

波长是一个波的两个峰之间的距离，在我们的例子中，到目前为止这是2π。这是因为要经历一个完整的波周期我们必须转一个角度2π。

我们也可以创造一个不同的波长λ， 这样需要将变量x乘以2π/λ以获得函数：

F(x)=sin(2πx/λ)

F(x)=cos(2πx/λ)

通过使波长变短，实际上是压缩了波，通过使波长变长，实际上是拉伸了波。

变高或变低

到目前为止，我们创建的波的峰值值为1，波谷值为-1。要创建一个波峰更高波谷更低的波，只需将整个函数乘以一个常数就可以得到：

F(x)=Asin(2πx/λ)

F(x)=Acos(2πx/λ)

这个常数A被称作波的振幅。

加速和减速

到目前为止，我们创造的波是静止的:它们不会随着时间而改变。然而，也有可能产生沿其行进的波。我们的波函数现在是两个变量的函数，两个变量分别是x和t，如前所述，x表示在横轴上的位置，而t表示时间。假设你想让波以函数的速度v移动:

以及

这些函数产生了这样的移动波。如果你让时间变量t保持固定，那么你本质上看到的是一个时间快照，给你一个静止波，就像我们上面看到的那样。如果您保持x在x-轴上的位置固定，那么您将看到相应的y-变量随着时间上下移动。这有点像看着湖面上的一个特定点随着波浪起伏而上下移动。

我们的函数现在的焦点是x-vt，在一段时间t内，波以速度v移动了一段距离vt，波在点处沿x-轴移动的高度，因此与时刻0时该点x-vt处的高度相同，因为这是波在时间t移动的距离。

本文内容由小洁整理编辑！