算出阴影部分的面积(小学题求阴影部分面积s)

导语：巧算阴影部分面积之和

上面的例题中我们讲述了如何计算阴影部分面积之差，今天我们来看看如何计算阴影部分面积之和。

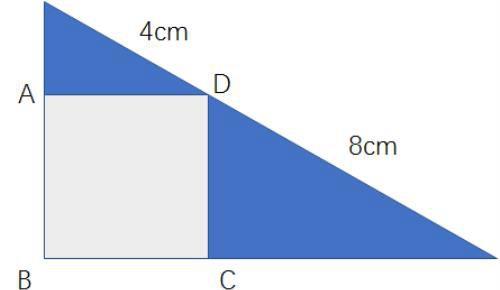
如图，一个大的直角三角形分成两个小的直角三角形和一个正方形（ABCD）。已知小直角三角形的斜边长为4cm，大直角三角形的斜边长为8cm，求此两个直角三角形的面积之和，即图中蓝色区域的面积之和。

这道题我们虽然知道了两个边的边长，但仔细观察发现，这两个边都是斜边，并不能构成底和高，也就是无法直接算出三角形的面积，那么应该如何是好呢？

我们可以将上面小直角三角形以D点为中心逆时针旋转90度，转到图中橘黄色的区域，这样，两个直角三角形就变成了一个大的直角三角形，而这个大的直角三角形的底和高分别是8cm和4cm，它的面积就是8×4÷2=16平方厘米。

那么，为什么上面小直角三角形能够恰好旋转到橘黄色区域呢？我们可以这样看，首先，ABCD是一个正方形，各边相等，四个角都等于90度，这样，AD以D为中心逆时针旋转90度就自然会落到CD边上，且与CD重合。

我们再来看角度关系，因为∠ADC=90°，所以∠1+∠2=90°，而∠1通过旋转到达了橘黄色区域内的∠1，因此，此时∠1+∠2=90°，因此，高等于4cm。

关 注 优博学园，学习更多数学知识

本文内容由快快网络小滢创作整理编辑！