考纲原文

（1）了解数列的概念和几种简单的表示方法（列表、图象、通项公式）.

（2）了解数列是自变量为正整数的一类函数.

知识点详解

一、数列的相关概念

1．数列的定义

3．数列的分类

二、数列的表示方法

（1）列举法：将数列中的每一项按照项的序号逐一写出，一般用于“杂乱无章”且项数较少的情况．

（2）解析法：主要有两种表示方法:

（3）图象法：数列是特殊的函数，可以用图象直观地表示．数列用图象表示时，可以以序号为横坐标，相应的项为纵坐标描点画图．由此可知，数列的图象是无限个或有限个孤立的点．

三、数列的前n项和与通项的关系

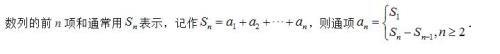
考向分析

考向一 已知数列的前几项求通项公式

1．常用方法：观察(观察规律)、比较(比较已知数列)、归纳、转化(转化为特殊数列)、联想(联想常见的数列)等方法．

具体策略：

①分式中分子、分母的特征；

②相邻项的变化特征；

③拆项后的特征；

④各项的符号特征和绝对值特征；

⑤化异为同．对于分式还可以考虑对分子、分母各个击破，或寻找分子、分母之间的关系；

3．根据图形特征求数列的通项公式，首先要观察图形，寻找相邻的两个图形之间的变化，其次要把这些变化同图形的序号联系起来，发现其中的规律，最后归纳猜想出通项公式．

考向三 由递推关系式求通项公式

递推公式和通项公式是数列的两种表示方法，它们都可以确定数列中的任意一项.高考对递推公式的考查难度适中，一般是通过变换转化成特殊的数列求解.

已知数列的递推公式求通项公式的常见类型及解法如下：

考向四 数列的性质

数列可以看作是一类特殊的函数，所以数列具备函数应有的性质，在高考中常考查数列的单调性、周期性等.

1．数列的周期性

先根据已知条件求出数列的前几项，确定数列的周期，再根据周期性求值．

2．数列的单调性

（1）数列单调性的判断方法：

（2）数列单调性的应用：

①构造函数，确定出函数的单调性，进而可求得数列中的最大项或最小项．

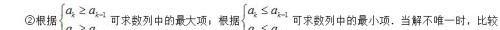
（3）已知数列的单调性求解某个参数的取值范围，一般有两种方法：

①利用数列的单调性构建不等式，然后将其转化为不等式的恒成立问题进行解决，也可通过分离参数将其转化为最值问题处理；

②利用数列与函数之间的特殊关系，将数列的单调性转化为相应函数的单调性，利用函数的性质求解参数的取值范围，但要注意数列通项中n的取值范围．

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小薇创作整理编辑！