无穷大的含义是什么(无穷大是存在吗)
导语:无穷大有多大?现实世界中,它应该在哪里?
引言
最初人们对无穷大的研究不是很深入,一句“多如牛毛”大致表达一下就可以了。听到的人同样也不会细究。大家都很有默契地保持了理解上的同步。
后来,康托尔对无穷大进行了比较系统的研究。无穷大的表达变得正式起来。康托尔之后,无穷大被越来越多的数学家所重视。目前主流的观点是:无穷大不是数,是一个大于任何数的抽象概念。
本人前面有两篇文章,探讨过无穷大,提出了一个关于无穷的处理模式。不过,前面两篇文章讲得不够透彻,只是本文的铺垫。本文将对无穷大展开深入讨论,并回答下面问题。
现实世界中,无穷大对应什么样的具体事物?
需要的两个基本共识
在深入讨论之前,就现代数学关于无穷大的认识,需要达成两个共识。这是讨论的基础。这两个共识是:
共识一,认可这个算式
共识二,认可如下的极限定义
定义
详述
广义定义
无限靠近而永远不能到达
数学上的定义
1. 极限是对变化过程的描述
2. 极限过程就是一个死循环
3. 极限过程不断接近确定值
4. 极限值是趋势上的预估值
从这两点可以看出来,在现代数学中,无穷大只是一个构想的概念。而且有下面两个特点。
无穷大在理论上已经约定好没有任何计算可以达到。无穷大只存在于构想中,不对应现实中的任何事物。从无穷大的这些特点,可以发现,平常我们描述或使用无穷大的一些话语,在数学上讲,就是错的。比如:
用“多如牛毛”来表达无穷大的意思。用“宇宙是无穷大的”来表达宇宙的大。这些话就如同“一望无际的大草原”一样,是一种夸张而富有诗意的表达,是经不起数学检验的。
我关于无穷大的观点
前面的两篇文章中,我提到了两个观点。
数应该同时具备物理基础和逻辑基础。无穷大需要和其他数放置在同一空间。空间在这里可以理解为容器或数轴。为支撑我的这些观点,前一篇文章,一步一步地从直线形数轴构造出了圆形数轴。如下图:
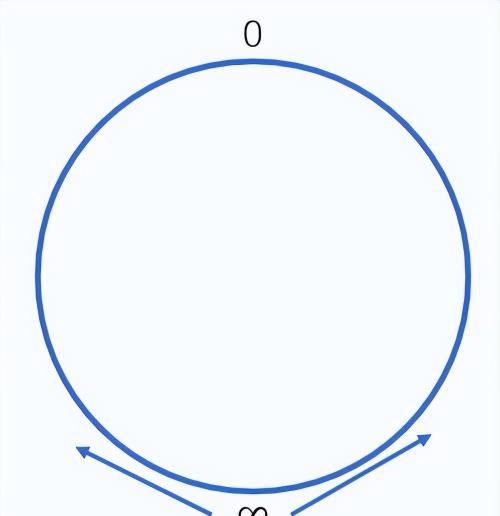
圆轴
这个圆形的数轴,我称之为“圆轴”。圆轴有两个特点:
原点对应无穷大圆轴有两个方向在圆轴中,无穷大是天然可达的。理由也很简单,“数轴的原点必定是可达的”。依据我的“数应该同时具备物理基础和逻辑基础”的观点,圆轴上的无穷大就必定可以在现实世界中找到对应的事物。
在现实世界中的无穷大
前面提到过,即便是以宇宙之大,相比于无穷大,那也是小了。这可以当做第一条线索。从圆轴上看,无穷大是距离原点最近的。这可以当做第二条线索。持有这两条线索,让我们放眼宇宙,找一找符合这两条线索的事物。
满足第一条线索的,应是我心。宇宙虽大,难比我心之大。纵有无穷宇宙纳入我心,亦是绰绰有余。心之大,堪比无穷大。
满足第二条线索的,亦应是我心。我心离我之近,那是完全没有距离的。这样分析后。假设以自己为原点,去考察整个宇宙。那么,我心就对应了无穷大。
我心在这里可以理解为大脑或者灵魂。
把我心对应无穷大,是我们在现实中找到的第一个无穷大。这可算做寻找无穷大之旅的第一步。
通过前面的寻找过程,可以发现,无穷大和两个事物相关。
要考察的对象原点的选择有了对无穷大、考察对象、原点这三者之间的关系的认识,就可以得出无穷大是和研究的具体问题是息息相关的结论。把握住这一点,在处理无穷大的时候,就可以同时把握无穷大的物理基础和逻辑基础了。
其实在现代数学的具体实践中,已经有人在使用圆轴系统的模式了。比如在人工智能领域,有一个数据规整化的处理。规整化,就是把拿到的数据统一转换为0-1之间的数。规整化之后,1事实上被当做无穷大处理了。
小结
区别于现代数数学的经典理论,圆轴系统中的无穷大,不再是一个孤零零的,逻辑上完全独立的概念。在圆轴系统中,每一个研究问题,都会有其自身的既有物理基础、又有逻辑基础的无穷大。理论上讲,不同问题领域的无穷大,在圆轴系统中,可以没有直接关联。
也正是基于这样的认识,在我前面的文章中,我才会多次把河图、洛书中的5这个数对应到无穷大。在我们国的传统文化中,把五对应无穷大做处理,是由来已久的。“九五之尊”这种说法,也是基于此理。
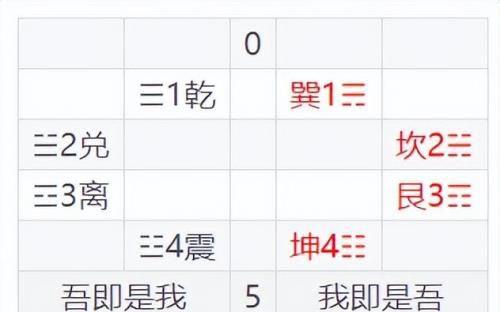
我即是无穷大
看了这篇文章后,如果有人和你说:因阳居正位,故有‘九五之尊’。你可以啐一口,并奉送其人两个字,酸儒。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小曲创作整理编辑!