高中物理极限法的含义(高中物理中的极限思想)

导语：高中物理（解题技巧）1——‘’极限法‘’的妙用

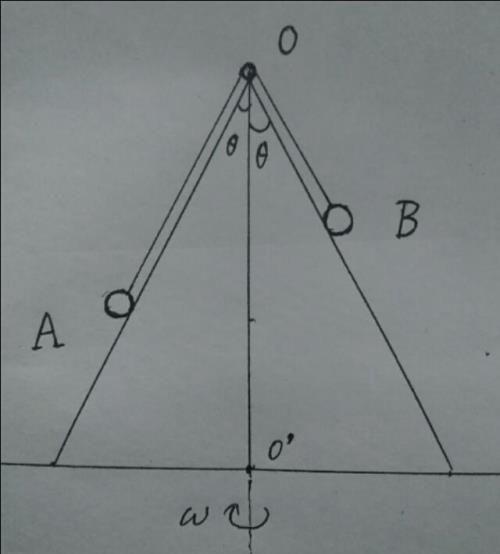
例题1. 如下图左，A、B两个小球用轻绳连接，轻绳跨过圆锥桶顶点处的小定滑轮，圆锥桶的侧面光滑，当圆锥桶绕竖直对称轴OO'匀速转动时，两个球都处于圆锥侧面上，且与桶保持相对静止。小球A到圆锥顶点O的距离大于B到O的距离，则下列判断正确的是：( )

A、A球的质量大

B、B球的质量大

C、A球对圆锥桶侧面的压力大

D、B球对圆锥桶侧面的压力大

《知识考查》：

本题是考查向心力知识，目的是考查应用数学知识解决物理问题的能力。

《解题思路》：

本题只需要判断出谁的质量大，就可以知道谁对圆锥侧面的压力大了，所以判断二者质量大小是关键。判断质量大小需要利用向心力知识列方程解决。

《一题多解》：

下面用两种解法解析此题，从中体会极限法的妙用。

1、常规接法：

先对小球受力分析，再进行正交分解，再列方程分析。

A、B两个球对绳子的拉力大小相等设为T，

圆锥侧面对球的支持力为F，

则有：Tcosθ＋Fsinθ＝mg ①

由上式可知，两个拉力T相等，

所以，m大，则F大，

Tsinθ－Fcosθ＝mω²Lsinθ ②

由②式可知，m大，F大，则L小。

所以可知B球的质量大，所以对圆锥侧面的压力也大。故BD正确。

2、特殊解法（极限法）

将图中圆锥角θ增大到90º，则两个圆锥侧面连成了一条直线，两个小球用一根轻绳连着，绕一个共同的圆心以共同的角速度转动，这就变成了‘’双星问题‘’，绳子拉力大小相等，提供各自的向心力，即 T＝mrω²，由式可知，r大，则m小，所以可得出，B球的r小，则B球的m大，对侧面的压力大，得出BD正确。

《总结》：常规法比较麻烦费时，但能考查出知识的掌握应用能力。

极限法简单省时，一个式子解决，但不容易想到。这个方法很好的考查了知识的灵活应用能力，拓宽了学生解题的思路，很好的提升了学生的解题能力。

《注意》：不是任何题都有技巧的，还是要掌握好基本的知识，基本的解题思路，做的题多了，思路就开阔了，有些方法技巧就会应用了。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小茜创作整理编辑！