六年级上册苏教版数学重点知识归纳(苏教版小学六年级上册数学知识点总结)
苏教版六年级数学上册知识点汇总
方程以及列方程解应用题
1、 形如ax±b=c方程的解法
【解方程时,可以利用等式的基本性质来解,注意两边要同时加上或减去同一个数】
2、 形如ax±bx=c方程的解法
【解方程时,第一步要把x前面的序数相加或相减,再
在两边同时除以同一个数】
3、 列方程解决实际问题
基本步骤:审清题意→找准等量关系→设未知数→列方程→解方程→检验→作答
基本类型:比较大小关系;总数和部分数关系;和倍与差倍关系;行程问题中的关系;涉及图形的周长、面积的关系等等。
长方体和正方体
1、 长方体和正方体的特征
形体
面
顶点
棱
关系
长方体
6个
至少4个面
是长方形
相对面
完全相同
8个
12
条
相对的棱
长度相等
正方体
是特殊
的长方
体
正方体
6个
正方形
6个面
完全相同
8个
12
条
12条长度
都相等
2、 表面积概念及计算 【长方体或正方体6个面的总面积,叫做它们的表面积】
算法:长方体 (长×宽+长×高+宽×高)×2
(ab+ah+bh)×2
正方体 棱长×棱长×6
a×a×6=6a2
注:不足6个面的实际问题根据具体情况计算,例如鱼缸、无盖纸盒等等。
3、 体积概念及计算
体积(容积)
定义
形体
体积(容积)
计算方法
体积单位
进率
物体所占空间的
大小叫做它们的
体积;容器所能
容纳其它物体的
体积叫做它的容
积。
长方
体
V=abh
V=Sh
立方米
立方分米
立方厘米
1
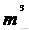
=1000

1

=1000

1L=1000mL
=1

正方
体
V=
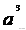
分数乘法
1、 分数乘法算式的意义:比如3×

表示3个

相加的和是多少,也可以表示3的

是多少
注:【求一个数的几分之几用乘法解答】
2、 分数与整数相乘:用整数与分数的分子相乘的积作为分子,分数的分母作为分母,最后约分成最简分数。或者先将整数与分数的分母进行约分,再应用前面计算法则。
注:【任何整数都可以看作为分母是1的分数】
3、 分数与分数相乘:用分子相乘的积作为分子,用分母相乘的积作为分母,最后约分成最简分数。
4、 分数连乘:通过几个分数的分子与分母直接约分再进行计算。
倒数的认识
1、 乘积是1的两个数互为倒数。
2、 求一个数(不为0)的倒数,只要将这个数的分子与分母交换位置。 【整数是分母为1的分数】
3、 1的倒数是1 , 0没有倒数。
4、 假分数的倒数都小于或等于1(或者说不大于1);
真分数的倒数都大于1。
分数除法
1、 分数除法计算法则:甲数除以乙数(不为0)等于甲数乘乙数的倒数。
2、 分数连除或乘除混合计算:可以从左向右依次计算,但一般是遇到除以一个数,把它改写成乘这个数的倒数来计算。
【转化成分数的连乘来计算】
3、 除数大于1,商小于被除数;除数小于1,商大于被除数;除数等于1,商等于被除数。
4、 分数除法的意义:已知一个数的几分之几是多少,求这个数可以用列方程的方法来解,也可以直接用除法。
注:在单位换算中,要弄清需要换算的单位之间的进率是多少。
认识比
1、 比的意义:比表示两个数相除的关系。
2、 比与分数、除法的关系:a:b=a÷b=

(b≠0)
相互关系
区别
比
前项
比号(:)
后项
比值
关系
分数
分子
分数线(-)
分母
分数值
数
除法
被除数
除号(÷)
除数
商
运算
3、 比值:比的前项除以比的后项,所得的商就叫比值。
注:比值是一个数,可以是整数、分数、小数,不带单位名称。
4、 比的基本性质:比的前项和后项同时乘或除以一个相同的数(0除外),比值不变。
5、 最简整数比:比的前项和后项是互质数。也就是比的前项和后项除了1意外没有其它公因数。
6、 化简:运用比的基本性质对比进行化简,方法:先把比的前、后项变成整数,再除以它们的最大公因数。
注:化简比和求比值是不同的两个概念【意义不同,方法不同,结果不同】
7、 按比例分配问题:将一个数量按照一定比例,分成几个部分,求每个部分是多少,这类问题称为按比例分配问题。
解决方法:先求出总份数,再求各部分数占总数的几分之几,转化成分数乘法来计算。
分数四则混合运算
1、 运算顺序:分数四则混合运算的顺序与整数相同。先算乘除法,后算加减法;有括号的先算括号里面的,后算括号外面的。
2、 运算律:加法的交换律:a+b=b+a
加法的结合律:(a+b)+c=a+(b+c)
乘法的交换律:a×b=b×a
乘法的结合律:(a×b)×c=a×(b×c)
乘法的分配律:(a+b)×c=a×c+b×c
3、 分数四则混合运算的应用题:
(1) 总数与部分数相比较的问题:【分数乘法、减法】
一般解题方法:先求出未知的部分数,再用总数减部分数等于另一部分数。
(2) 已知一个数量比另一个数量多(或少)几分之几,求这个数量是多少的问题:【分数乘法、加减法】
一般解题方法:先求出多(或少)的部分,再用加法或减法求出结果。
注:对于题中出现的带单位与不带单位的分数,要注意它们的意义不一样。
解决问题的策略
1、 用“替换”策略解决实际问题
2、 用“假设”策略解决实际问题
可能性
用分数来表示可能性的大小:

认识百分数
1、 百分数的意义:表示一个数是另一个数的百分之几的数叫做百分数,也叫百分比或百分率。
2、 百分数的读写:百分数不写成分数形式,先写分子,再写百分号。
注:百分数后面不带单位名称。(常出现在判断题中)
3、 百分数与小数的互化:
去掉百分号,再将小数点向左移动两位
百分数

小数
将小数点向右移动两位,再在后面添上℅
4、 百分数与分数的互化:
先改写成分母是100的分数,再约分成最简分数
百分数

分数
先将分数化成小数(遇到除不尽时,一般保留三位小数)。再改写成百分数
5、 百分数应用题:
一般解题方法:求一个数是另一个数的百分之几,用除法计算。
注:理解生活中常见的一些百分率。例如:出勤率、发芽率、成活率、合格率、含盐率、普及率等等。
免责声明:本文内容由互联网优秀作者用户自发贡献,本站仅提供存储空间服务,不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容,请与我们取得联系举报,一经查实立刻删除内容。本文内容由快快网络小涵创作整理编辑!