二次函数中平行四边形的存在性问题解析(二次函数中平行四边形的存在性问题解析图)
导语:二次函数中平行四边形的存在性问题解析
二次函数的图象
二次函数解析式的三种形式
1、一般式:y = ax2 + bx + c ( a , b , c 为常数,a ≠ 0 );
2、顶点式:y = a( x - h )2 + k ( a , b , c 为常数,a ≠ 0 );
3、两点式:y = a( x - x1 )( x - x2 )( a ≠ 0 ).
平行四边形的判定方法及性质
平行四边形
1、平行四边形的判定方法
定义:两组对边分别平行的四边形是平行四边形;
定理 1:两组对角分别相等的四边形是平行四边形;
定理 2:两组对边分别相等的四边形是平行四边形;
定理 3:对角线互相平分的四边形是平行四边形;
定理 4:一组对边平行且相等的四边形是平行四边形 .
2、平行四边形的性质
性质 1:平行四边形的邻角互补,对角相等;
性质 2:平行四边形的对边平行且相等;
性质 3:平行四边形的对角线互相平分.
二次函数中平行四边形的存在性问题

二次函数中平行四边形的存在性问题
学习目标:
1、会用分类思想讨论平行四边形的存在问题;
2、会用数形结合的思想解决综合性问题.
重点:分类讨论平行四边形的存在性;
难点:数形结合思想及画图.
一、知识回顾(储备)
1、线段的中点坐标公式
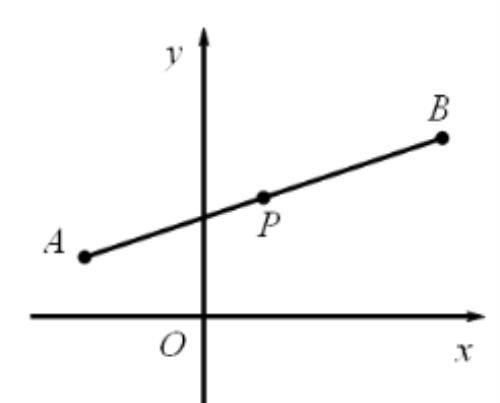
线段的中点坐标公式
在平面直角坐标系中,有任意两点 A、B,若点 A 坐标为 (x1,y1),点 B 坐标为 (x2,y2),
则线段 AB 的中点 P 的坐标为 (( x1 + x2 )/ 2 , ( x1 + x2 )/ 2 ) .
2、知识拓展与应用:
思考:在平面直角坐标系中,□ABCD 的顶点坐标分别为 A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
已知其中 3 个顶点的坐标,如何确定第 4 个顶点的坐标 ?
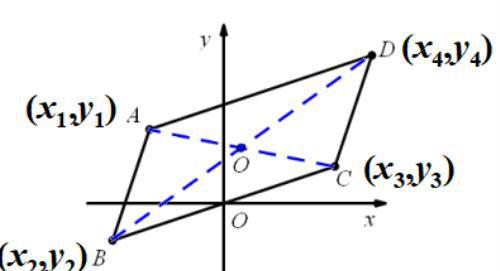
引例:如图,已知 □ABCD 中 A (-2,2),B (-3,-1), C (3,1),则点 D 的坐标是 (4,4) .
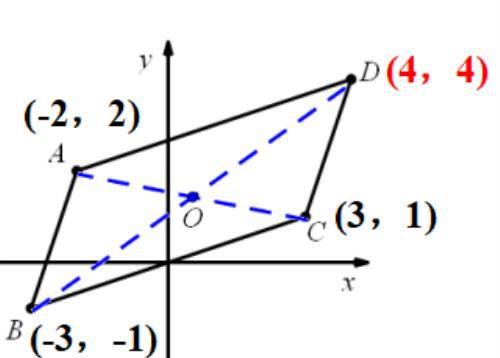
利用中点公式分析: ( x1 + x3 )/ 2 = ( x2 + x4 )/ 2 , ( y1 + y3 )/ 2 = ( y2 + y4 )/ 2 .
结果化简可以化为 “ 对点法 ” 的形式 : x1 + x3 = x2 + x4 , y1 + y3 = y2 + y4 .
二、对点法( 数学方法 )
如图,在平面直角坐标系中,□ABCD 的顶点坐标分别为 A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
则这 4 个顶点坐标之间的关系是什么?

结论:x1 + x3 = x2 + x4 ,y1 + y3 = y2 + y4 .
平面直角坐标系中,平行四边形两组相对顶点的横坐标之和相等,纵坐标之和也相等.
三、典例学习( 三定一动 )
【例1】如图,在平面直角坐标系中,已知 A (-1,0),B (1,-2), C (3,1),点 D 是平面内一动点,
若以点 A 、B 、 C、 D 为顶点的四边形是平行四边形,则点 D 的坐标是 ______.
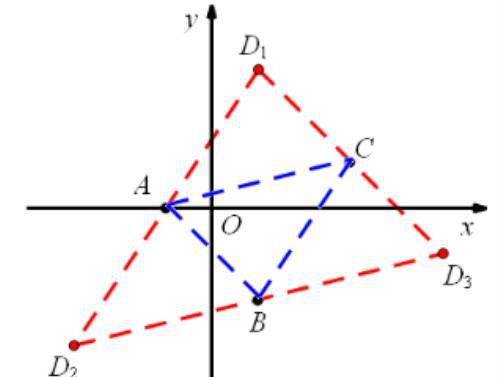
分析:设点 D(x,y),
① 点 A 与点 B 相对:
-1 + 1 = 3 + x,0 - 2 = 1 + y;x = -3,y= -3 ,此时 D2(-3,-3);
② 点 A 与点 C 相对:
-1 + 3 = 1 + x,0 + 1 = -2 + y;x = 1,y = 3,此时 D1(1,3);
③ 点 A 与点 D 相对:
-1 + x = 1 + 3,0 + y = -2 + 1;x = 5,y = -1,此时 D3(5,-1);
综上所述:点 D 的坐标是 (-3,-3),(1,3), (5,-1) .
说明:( 细节 )
若题中四边形 ABCD 是平行四边形,则点 D(1,3),与四个点为顶点的四边形是平行四边形不同.
四、问题解决
【例题2】已知,抛物线 y = - x2 + x +2 与 x 轴的交点为 A、B,与 y 轴的交点为 C,点 M 是平面内一动点,若以点 M、A、B、C 为顶点的四边形是平行四边形,请写出点 M 的坐标.
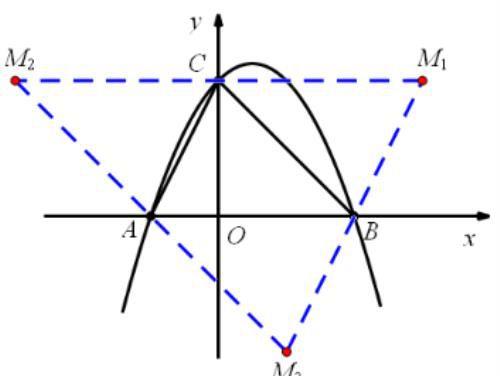
解析:( 三定一动 )
先求出 A( -1,0 ),B ( 2,0 ),C( 0,2 ),设点 M(x,y),
① 点 A 与点 B 相对:M3(1,-2);
② 点 A 与点 C 相对:M2(-3,2);
③ 点 A 与点 M 相对:M1(3,2);
综上所述:点 M 的坐标是 M1(3,2),M2(-3,2),M3(1,-2).
【例题3】如图,平面直角坐标中,y = - 0.25x2 + x 与 x 轴相交于点 B (4,0),点 Q 在抛物线的对称轴上,点 P 在抛物线上,且以点 O、B、Q、D 为顶点的四边形是平行四边形,写出相应的点 P 的坐标 .
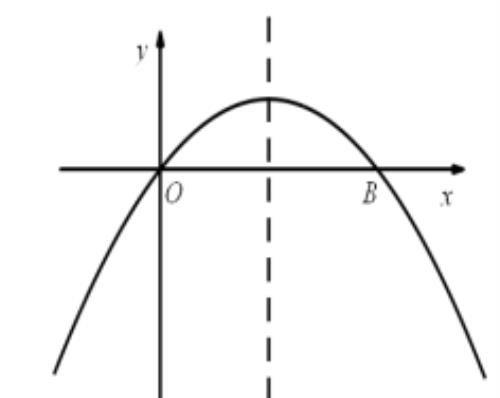
解析:( 两定两动其中一点为半动点 )
已知 B (4,0),O(0,0),设 Q ( 2, a ),P ( m, -0.25m2 + m ).
① 点 B 与点 O 相对:m = 2,a = -1;P1(2,1);
② 点 B 与点 Q 相对:m = 6,a = -3;P2(6,-3);
③ 点 B 与点 P 相对:m = -2,a = -3;P3(-2,-3);
综上所述:P1(2,1),P2(6,-3),P3(-2,-3).
【例题4】如图,平面直角坐标中,y = 0.5x2 + x - 4 与 y 轴相交于点 B (0,-4),点 P 是抛物线上的动点,点 Q 是直线 y = - x 上的动点,判断有几个位置能使以点 P、Q、B、O 为顶点的四边形为平行四边形,写出相应的点 Q 的坐标.
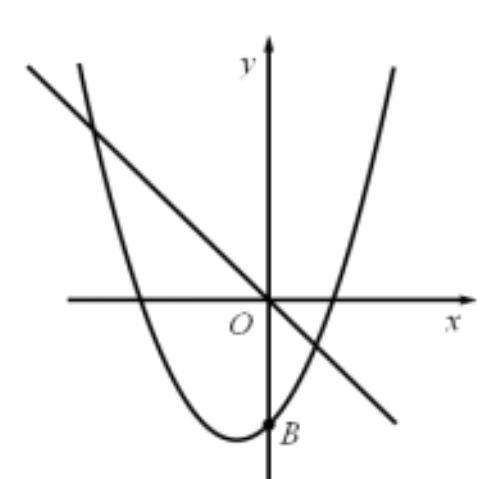
解析:( 两定两动 )
已知 B (0,-4),O(0,0),设 P ( m, 0.5m2 + m - 4 ),Q ( a, -a ).
① 点 B 与点 O 相对:a1 = 4 , a2 = 0 ( 舍 );
② 点 B 与点 P 相对:a = -2 ± 2√5 ;
③ 点 B 与点 Q 相对:a1 = - 4 , a2 = 0 ( 舍 );
综上所述:
Q1( -2 + 2√5 ,2 - 2√5 ),Q2(-2 - 2√5 ,2 + 2√5 ),Q3(-4,4), Q4( 4,-4 ).
五、总结
“ 对点法 ”,需要分三种情况,得出三个方程组求解,动点越多,优越性越突出!
从“几何” 的角度解决问题的方法,能够使问题直观呈现,问题较简单时,优越性较突出!
“数无形时不直观,形无数时难入微”,数形结合是一种好的解决问题的方法!
六、作业(略)。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小快创作整理编辑!