跟三角形中线角平分线高线有关的常见模型(三角形的中线角平分线高线的特点)

导语：跟三角形中线、角平分线、高线有关的常见模型和结论总结

三角形的概念

三角形边、角之间的关系：①任意两边之和大于第三边（任意两边之差小于第三边）；②三角形内角和为180°

（外角和为360°）；③三角形的外角等于不相邻的两内角和。

三角形的中线

（1）定义：三角形的顶点和对边中点的连线叫三角形的中线。

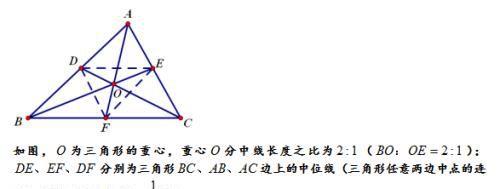
（2）性质：三角形三边中线交于一点，叫三角形的重心，三角形的重心分中线之比为2:1。

三角形中心的性质

几何问题中的“中点”与“中线”常常是联系再一起的。因此遇到中点这样的条件（或关键词）我们可以考虑中线定理与中位线定理进行思考。

（3）中线（中点）的应用：

三角形中线应用

三角形的角平分线

(1）定义：三角形三内角的角平分线与对边交点所构成的线段叫三角形的角平分线。

（2）性质：三角形的三条内角平分线交于一点，叫三角形的内心（即三角形内切圆的圆心）。三角形的内心到三边的距离相等。

三角形内心性质

（3）关于角平分线角度问题的常见结论：（其中BO和CO都是三角形内角或外角平分线）

角平分线角度问题的常见图形结论

（4）角平分线的性质定理：角平分线上的点到角两边的距离相等；到角两边距离相等的点在这个角的角平分线上。

三角形角平分线性质定理

三角形的高线

（1）定义：三角形顶点到对边的垂线叫三角形的高线。

（2）性质：三角形三条边上的高交于一点，叫三角形的垂心。（锐角三角形的垂心在形内，钝角三角形的垂心在形外，直角三角形的垂心是直角顶点。）

三角形的高线

特别注意：在等腰三角形中，我们通常所指的三线合一就是指中线、角平分线、高线。三线合一：已知三角形三线中的任意两个条件是重合的，那么就可以得出第三条线也是重合的。在具体运用时，我们往往时把三线合一的等腰三角形补充完整再加以运用。

三角形

本文内容由小彤整理编辑！