函数的自变量一定是x吗(函数的自变量不是x为什么的区别)
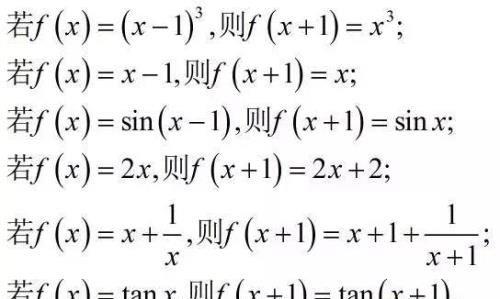
导语:高考数学:函数的自变量到底是不是x?
对于:很多同学一直没明白这么一个题,若f(x+1)是奇函数,为什么f(-x+1)=-f(x+1)。总觉得是应该(x+1)吧都变为-的,为什么不能当整体呢?
看下面的例题:
从以上例题看出两点:
1.f(x+1)为奇函数不等于f(x)为奇函数;反过来,f(x)为奇函数也不等于f(x+1)为奇函数。也就是说,f(x)为奇函数和f(x+1)为奇函数是两回事。
通常情况下,如果没有周期的话,f(x)和f(x+1)不太可能同时为奇函数,毕竟要平移一个单位。如果其中一个函数为奇函数,图象关于(0,0)对称,平移一个单位之后,对称中心就不再是(0,0)了。
2.不管是f(x)还是f(x+1),函数的自变量始终是x。看上面的六个例子,是不是这样?
如果承认第2点的事实,那么根据奇函数的定义:自变量相反,则函数值相反。
所以f(x+1)为奇函数等价于f(-x+1)=-f(x+1)。
可以当作整体呢?
当然可以。
令x+1=t,则f(x+1)就转化为f(t).那么f(x+1)为奇函数是否意味着f(t)为奇函数呢?
如果你回答“是”,那就与我上面讲的第1点矛盾。
也就是说,通过代换,你竟然可以把f(x+1)为奇函数变为f(x)为奇函数?
错在哪里呢?
脑中始终要有自变量的概念,说函数是否为奇偶函数之前,要确定哪个是自变量,即确定是关于哪个自变量的奇偶函数。
举个例子就明白了。
f(x+1)是关于x的函数,同时是关于x的奇函数;f(t)是关于t的函数,但不是关于t的奇函数。
所以,为了让你脑中始终铭记f(x+1)是关于自变量x的函数,我建议这样处理:避免错误的最佳方法:构造新函数,或者用平移的观点
当然,从图象平移的角度更好理解。
f(-x+1)=-f(x+1)所表达的函数特征,也是图象关于(1,0)对称。
本文内容由小故整理编辑!