导语：八年级上册数学期中测试试卷（含答案）

八年级上册数学期中测试

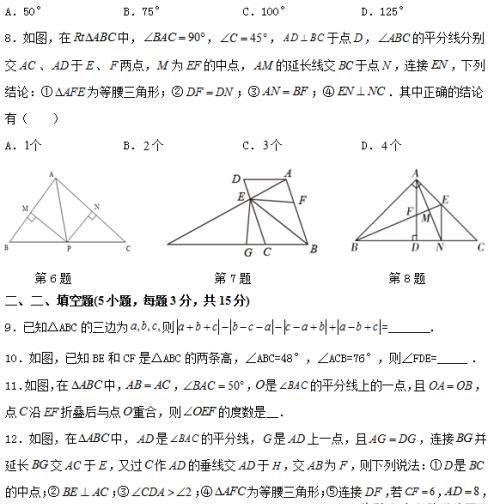
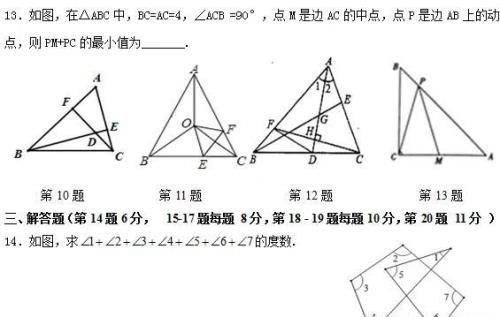
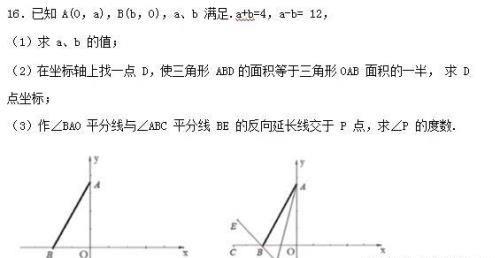
参考答案

1．A 【解析】

如图，延长AP与BC相交于点D，

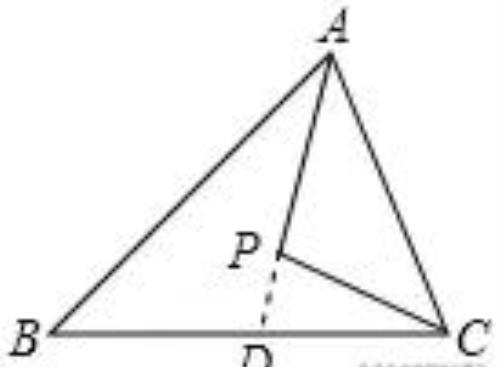
由三角形的外角性质得，∠PDC>∠B，∠APC>∠PDC，

所以，∠APC>∠B.

故选A.

点睛：三角形的外角大于任何一个和它不相邻的内角.

2．A

【解析】根据轴对称图形的概念求解．

故选：A.

【点睛】此题考查轴对称的概念．解题关键在于掌握轴对称的关键是寻找对称轴，两边图象折叠后可重合．

3．B【详解】

∵∠AOB＝∠COD＝36°，

∴∠AOB＋∠BOC＝∠COD＋∠BOC，

即∠AOC＝∠BOD，

在△AOC和△BOD中

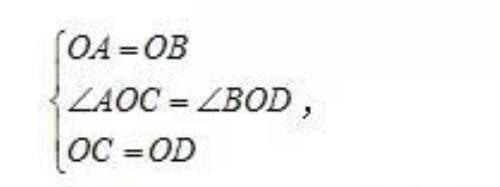
∴△AOC≌△BOD（SAS），

∴∠OCA＝∠ODB，AC＝BD，②正确；

∴∠OAC＝∠OBD，

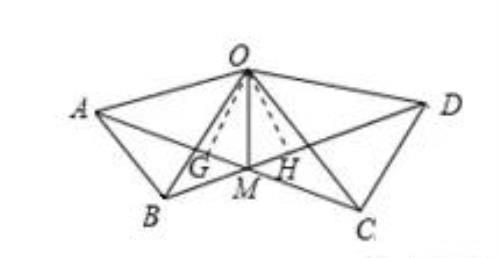
由三角形的外角性质得：∠AMB＋∠OBD＝∠AOB＋∠OAC，

∴∠AMB＝∠AOB＝36°，②正确；

作OG⊥AC于G，OH⊥BD于H，如图所示：

则∠OGC＝∠OHD＝90°，

在△OCG和△ODH中，

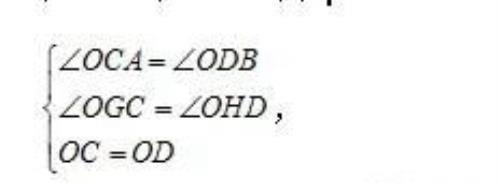
∴△OCG≌△ODH（AAS），

∴OG＝OH，

∴平分，④正确；

∵∠AOB＝∠COD，

∴当∠DOM＝∠AOM时，OM才平分∠BOC，

假设∠DOM＝∠AOM

∵△AOC≌△BOD，

∴∠COM＝∠BOM，

∵MO平分∠BMC，

∴∠CMO＝∠BMO，

在△COM和△BOM中，

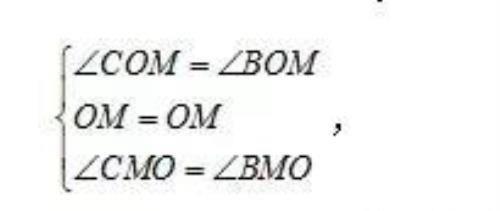
∴△COM≌△BOM（ASA），

∴OB＝OC，

∵OA＝OB

∴OA＝OC

与矛盾，

∴③错误；

正确的有①②④；

故选B．

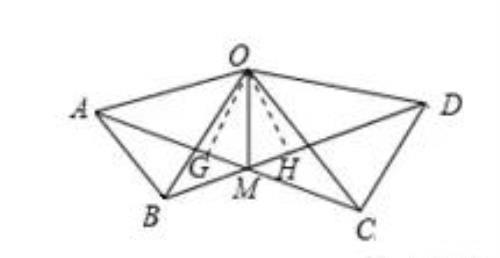
【点睛】

本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识；证明三角形全等是解题的关键．

4．B【分析】

如图:作GE⊥AD于E，EG的延长线交BC于F，由平行线的性质可得EF⊥BC，再根据角平分线的性质可得GE=GH=5，G F=GH=5，EF的长即为所求．

【详解】

解：如图：作GE⊥AD于E，EG的延长线交BC于F，则∠DEG=90°

∵AD//BC

∴∠BFG=∠DEG=90°

∴EF⊥BC

∵BC，AG分别平分∠ABC与∠BAD

∴GE=GH=5，G F=GH=5

∴EF=5+5=10，即AD与BC之间的距离为10．

故选：B．

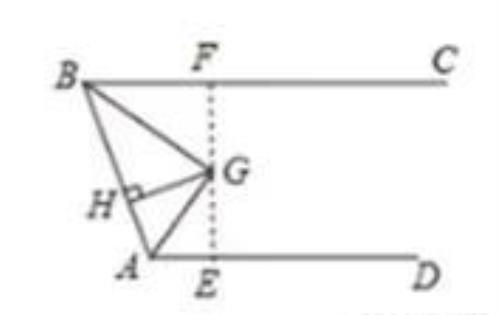
【点睛】

本题考查了角平分线的性质和平行线的性质，作出辅助线并掌握角的平分线上的点到角的两边的距离相等是解答本题的关键．

5．B【分析】

经过第一次操作可知剩下的长方形一边长为a，另一边长为2﹣a；若第二次操作后，剩下的长方形恰好是正方形，则所以剩下的长方形的两边分别为2﹣a、a﹣（2﹣a）＝2a﹣2；根据第2次剩下的长方形分两种情况讨论，若第三次操作后，剩下的长方形恰好是正方形，由此可得出关于a的一元一次方程，解之即可得出结论．

【详解】

解：第1次操作，剪下的正方形边长为a，剩下的长方形的长宽分别为a、2﹣a，由1＜a＜2，得a＞2﹣a；第2次操作，剪下的正方形边长为2﹣a，所以剩下的长方形的两边分别为2﹣a、a﹣（2﹣a）＝2a﹣2，

①当2a﹣2＜2﹣a，即a＜时，

则第3次操作时，剪下的正方形边长为2a﹣2，剩下的长方形的两边分别为2a﹣2、（2﹣a）﹣（2a﹣2）＝4﹣3a，则2a﹣2＝4﹣3a，解得a＝1.2；

②2a﹣2＞2﹣a，即a＞时

则第3次操作时，剪下的正方形边长为2﹣a，剩下的长方形的两边分别为2﹣a、（2a﹣2）﹣（2﹣a）＝3a﹣4，则2﹣a＝3a﹣4，解得a＝1.5．

故选：B．

【点睛】

本题考查数式规律、图形规律、一元一次方程等知识，其中涉及分类讨论法思想，综合性较强，有点难度，认真审题寻找规律，掌握相关知识是解题的关键.

【详解】

解：如图：作AD⊥BC与点D，

∵是的角平分线，，分别是，的高，

∴PM=PN，

∵∠AMP=∠ANP=90°，AP为公共边，

∴△APM≌△APN，

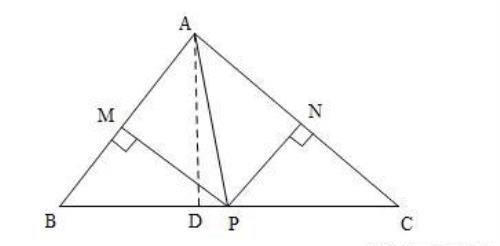
【点睛】

本题考查了角平分线的性质定理，全等三角形的判定，三角形的面积公式，解题的关键是熟练掌握角平分线的性质定理和三角形的面积公式进行解题．

7．C【分析】

∠BEG=∠FEG-∠FEB=，∠AEF=180°-∠FEG-∠HEG=180°-2β，在△AEF中，，AD∥BC，∠D=∠ABC，得到AB∥CD，由平行线的性质和邻补角的定义即可求解．

【详解】

解：设∠FBE=∠FEB=α，则∠AFE=2α，

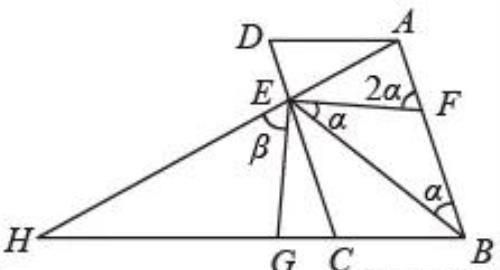
∠FEH的角平分线为EG，设∠GEH=∠GEF=β，

∵AD∥BC，

∴∠ABC+∠BAD=180°，

∵∠D=∠ABC，

∴∠D+∠BAD=180°，

∴AB∥CD，

∵∠BEG=40°，

∴∠BEG=∠FEG-∠FEB=β-α=40°，

∵∠AEF=180°-∠FEG-∠HEG=180°-2β，

在△AEF中，180°-2β+2α+∠FAE=180°，

∴∠FAE=2β-2α=2（β-α）=80°，

∵AB∥CD，

∴∠CEH=∠FAE=80°，

∴∠DEH=180°-∠CEH=100°．

故选：C．

【点睛】

本题考查的是平行线的性质，涉及到角平行线性质定理、三角形外角定理，本题关键是用有关α，β的等式表示出△AEF内角和为180°，题目难度较大．

8．D【分析】

①由等腰直角三角形的性质得∠BAD=∠CAD=∠C=45°，再根据三角形外角性质可得到∠AEF=∠AFE，可判断△AEF为等腰三角形，于是可对①进行判断；求出BD=AD，∠DBF=∠DAN，∠BDF=∠ADN，证△DFB≌△DAN，即可判断②③；连接EN，只要证明△ABE≌△NBE，即可推出∠ENB=∠EAB=90°，由此可知判断④．

【详解】

解：∵等腰Rt△ABC中，∠BAC=90°，AD⊥BC，

∴∠BAD=∠CAD=∠C=45°，BD=AD，

∵BE平分∠ABC，

∴∠ABE=∠CBE=∠ABC=22.5°，

∴∠AEF=∠CBE+∠C=22.5°+45°=67.5°，

∠AFE=∠FBA+∠BAF=22.5°+45°=67.5°，

∴∠AEF=∠AFE，

∴AF=AE，即△AEF为等腰三角形，所以①正确；

∵为的中点，

∴AM⊥BE，

∴∠AMF=∠AME=90°，

∴∠DAN=90°−67.5°=22.5°=∠MBN，

在△FBD和△NAD中

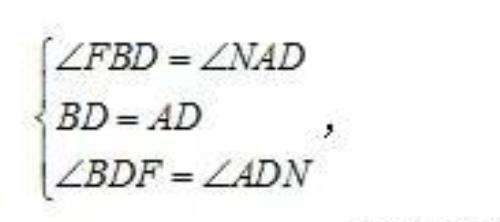
∴△FBD≌△NAD（ASA），

∴DF=DN，AN=BF，所以②③正确；

∵AM⊥EF，

∴∠BMA=∠BMN=90°，

∵BM=BM，∠MBA=∠MBN，

∴△MBA≌△MBN，

∴AM=MN，

∴BE垂直平分线段AN，

∴AB=BN，EA=EN，

∵BE=BE，

∴△ABE≌△NBE，

∴∠ENB=∠EAB=90°，

∴EN⊥NC，故④正确，

故选：D．

【点睛】

本题考查了全等三角形的判定与性质、三角形外角性质、三角形内角和定理、垂直平分线的性质，能正确证明推出两个三角形全等是解此题的关键，主要考查学生的推理能力．

【点睛】

本题主要考查了三角形三边的关系以及绝对值化简的基本方法，熟练掌握相关概念是关键

10．124°【详解】

试题解析：在△ABC中， ∵∠A+∠ABC+∠ACB=180°，

∴∠A=180°﹣48°﹣76°=56°，

在四边形AFDE中，

∵∠A+∠AFC+∠AEB+∠FDE=360°，

又∵∠AFC=∠AEB=90°，∠A=56°，

∴∠FDE=360°﹣90°﹣90°﹣56°

=124°.

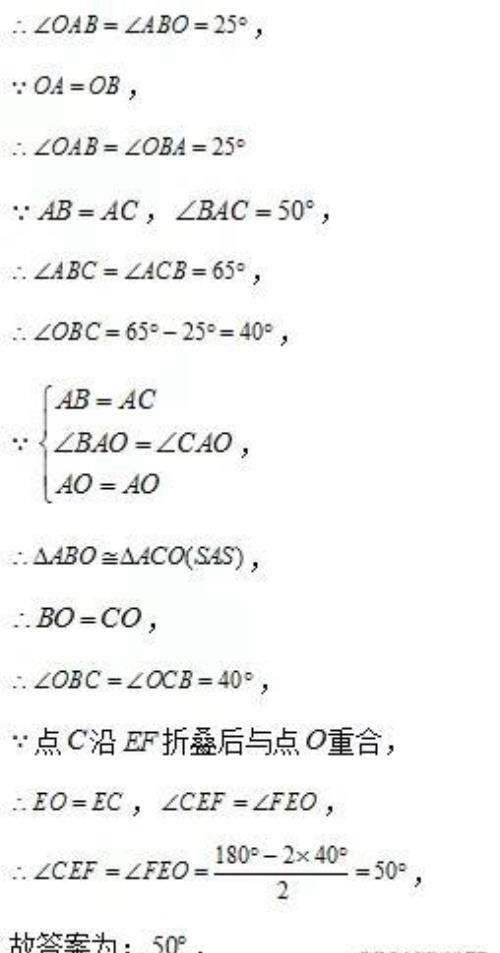
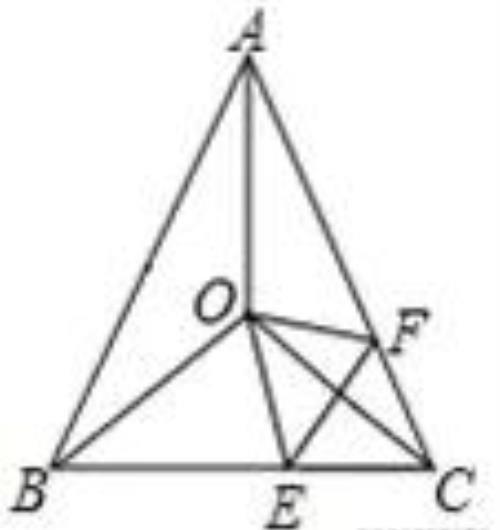
此题主要考查了翻折变换的性质以及全等三角形的性质和三角形内角和定理等知识，利用翻折变换的性质得出对应相等关系是解题关键．

12．③④⑤【分析】

根据等腰三角形的定义、三角形的中线、三角形的高的概念进行判断，对角线垂直的四边形的面积=对角线乘积的一半；分别对选项进行判断，即可得到答案.

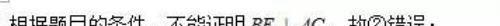
∵∠ADC=∠1+∠ABD，∠1=∠2，

∴∠ADC＞∠2，故③正确；

∵∠1=∠2，AH=AH，∠AHF=∠AHC=90°，

∴△AHF≌△AHC（ASA），

∴AF=AC，故④正确；

∵AD⊥CF，

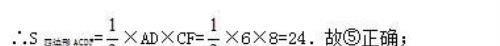
∴正确的有：③④⑤；

故答案为：③④⑤.

【点睛】

本题考查了三角形的角平分线、三角形的中线、三角形的高的概念，对角线垂直的四边形的面积，注意：三角形的角平分线、中线、高都是线段，且都是顶点和三角形的某条边相交的交点之间的线段．透彻理解定义是解题的关键．

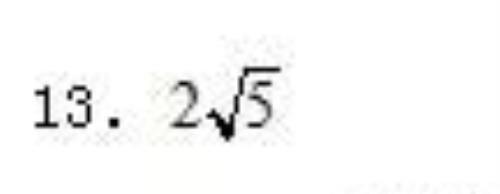
【解析】

试题分析：作点C关于AB的对称点C′，连接C′M与AB交于点P，连接PM、PC．此时PM+PC= C′M最小，在Rt△BM C′中利用勾股定理即可求出最小值．

解：作点C关于AB的对称点C′交AB于点O，连接C′M与AB交于点P，连接PM、PC、C′B ,此时PM+PC= C′M最小.

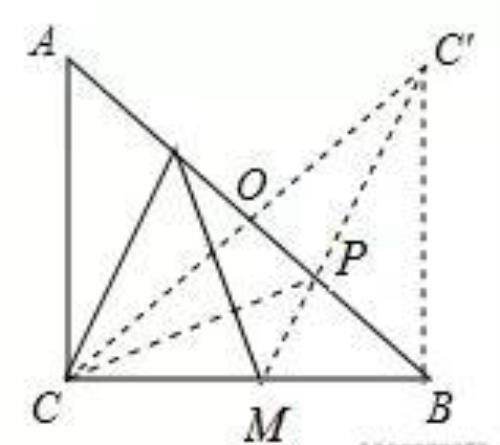
由对称性可知∠C′BP=∠CBP=45°，

∴∠CBC′=90°，

∴BC′⊥BC,∠BCC′=∠BC′C=45°，

∴BC′=BC=4，

∵M是BC边的中点，

∴BM=2，

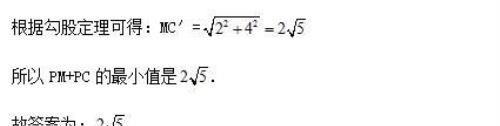
点睛：本题主要考查轴对称的性质、正方形的性质和勾股定理.作点C关于AB的对称点C′从而构造最短路径是解题的关键.

14．540°．【分析】

首先根据三角形的外角的性质，可得∠10=∠1+∠9，∠11=∠1+∠8，所以∠10+∠11=∠1+∠9+∠1+∠8=180°+∠1；然后求出（∠2+∠3+∠4+∠11）+（∠5+∠6+∠7+∠10）的度数，再用所得的结果减去180°，求出∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数是多少即可．

【详解】

解：如图1，

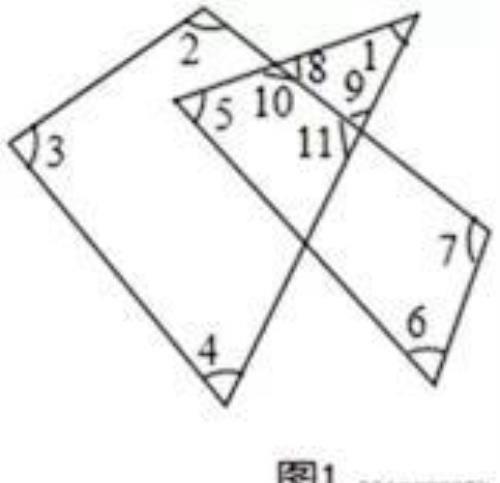
∵∠10=∠1+∠9，∠11=∠1+∠8，

∴∠10+∠11=∠1+∠9+∠1+∠8=180°+∠1，

∴（∠2+∠3+∠4+∠11）+（∠5+∠6+∠7+∠10）

=360°+360°

=720°

∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=720°-180°=540°，

即∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数是540°．

故答案为：540°．

【点睛】

本题考查多边形的内角和外角，三角形的内角和定理，熟练掌握内角和定理是解题的关键．

15．（1）作图见解析；（2）作图见解析；（3）证明见解析.

【分析】

（1）尺规作图找出AC的中点D，连结BD，则△BAD和△BCD为偏等积三角形．

（2）利用“偏等积三角形”的定义得出，△ABC与△DEF为“偏等积三角形”．

（3）过点B作BH⊥AE，垂足为H，先证明△ABH≌△ACD，则CD=HB．，依据三角形的面积公

式可知S△ABE=S△CDA，然后再依据偏等积三角形的定义进行证明即可．

【详解】

（1）如图1所示，△ABD和△BCD是偏等积三角形；

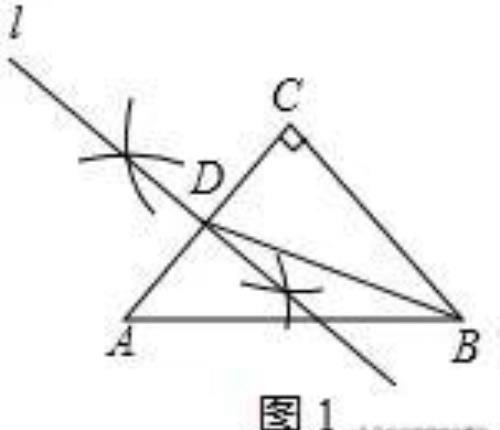
（2）如图2所示，△ABC和△DEF是偏等积三角形；

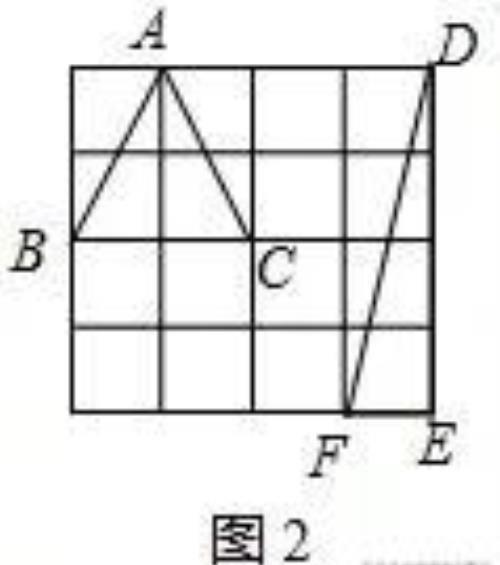
（3）如图3所示：过点B作BH⊥AE，垂足为H．

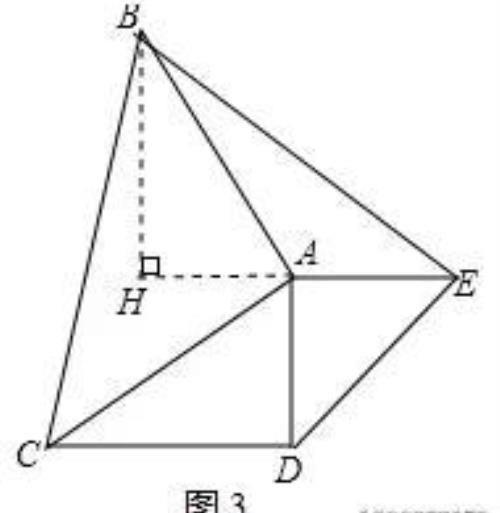
∵等腰直角三角形ABC和等腰直角三角形ADE，∠CAB=∠DAE=90°，

∴∠HAC+∠DAC=90°，∠BAH+∠HAC=90°．

∴∠BAH=∠DAC．

在△ABH和△ACD中

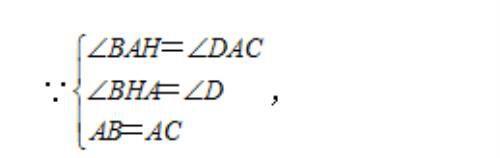
∴△ABH≌△ACD（AAS），

∴BH=CD，

∵S△ABE=BH•AE，S△ACD=AD•CD，

∵AE=AD，CD=BH，

∴S△ABE=S△ACD，

又由图知，这两个三角形不全等，

∴△ACD与△ABE为偏等积三角形．

【点睛】

本题主要考查作图-应用与设计作图，解题的关键是理解并掌握偏等积三角形的概念，熟练掌握中垂线的尺规作图，全等三角形的判定与性质，等腰三角形的性质等知识点．

16．（1）a=8，b=-4；（2）D(-2,0) 或(-8,0)或(0,4) 或(0，16);（3）45°．

【解析】

（1）根据已知列方程组即可求出a、b的值

（2）分点D在x轴上和y轴上进行解答即可

（3）根据三角形的一个外角等于与它不相邻的两个内角的和，列式求出∠ABC，再根据角平分线的定义求出∠ABE和∠BAP，然后根据三角形的一个外角等于与它不相邻的两个内角的和，列式计算即可得解．

【详解】

解：（1）∵a+b=4，a-b= 12，

∴a=8，b=-4

（2）当点D在x轴上时，

∵三角形ABD 的面积等于三角形OAB 面积的一半，

∴D为OB的中点或BD=OB,∴D(-2,0)或(-8,0)

当点D在y轴上时，

∵三角形ABD 的面积等于三角形OAB 面积的一半，

∴D为OA的中点或OA=AD，∴D(0,4)或(0，16)

∴D(-2,0) 或(-8,0)或(0,4) 或(0，16)

（3）根据三角形的外角性质，可得∠ABC=∠AOB+∠BAO，

∵BE平分∠CBA，AP平分∠BAO，

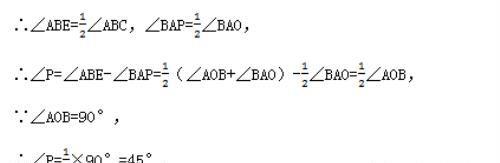
【点睛】

本题主要考查了三角形外角的性质，三角形中线的性质，解题的关键是能把三角形的外角和角的平分线相结合．

17．见详解.

【分析】

（1）要证，利用等角对等边只需证出∠AFE=∠AEF，利用平行不难发现这两个角和角平分线分成的两角是内错角和同位角；

（2）利用倍长中线法构造出全等三角形即可.

【详解】

证明：（1）∵MF∥DA

∴∠AFE=∠CAD，∠AEF=∠DAE

又∵AD平分∠CAB

∴∠CAD=∠DAE

∴∠AFE=∠AEF

∴AE=AF

（2）将FM延长至N使FM=MN，连接BN.

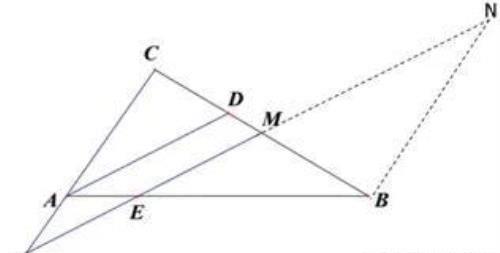
∵M为CB中点

∴CM=MB

在△FMC和△NMB中

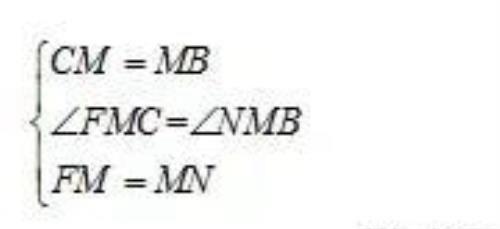
∴△FMC≌△NMB（SAS）

∴CF=BN，∠F=∠N

又∵∠AFE=∠AEF，∠AEF=∠BEN

∴∠N=∠BEN

∴BE=BN

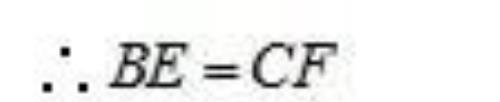
【点睛】

此题考查的（1）平行线的性质和等角对等边；（2）倍长中线法构造全等三角形.

18．（1）130°，20°；（2）36°．

【分析】

（1）根据题意画出图形，确定伴生角∠B=30°，根据等腰三角形性质和三角形内角和即可求解；

（2）根据题意画出图形，确定伴生角为∠B，题目中有三个等腰三角形，得到∠B=∠BAD，∠ADC=∠C=2∠B，根据三角形内角和即可求解

【详解】

解：（1）如图，△ABC和△ABD中，AB=AB，AD=AC，∠B=∠B，则△ABC和△ABD是伴生三角形，其中∠B为伴生角，当∠B为50°时，无法画出图形，当∠B=30°，∠C=50°．

∵AD=AC，

∴∠C=∠ADC=50°，

∴∠ADB=130°，

∴∠BAD=180°-∠B-∠ADB=20°．

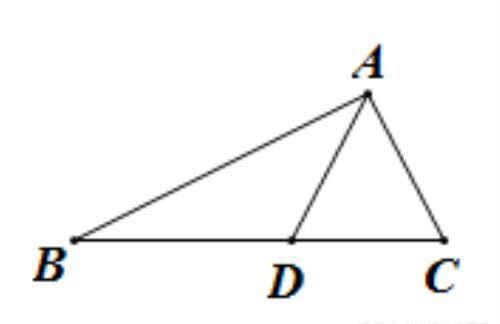
故答案为：130°，20°；

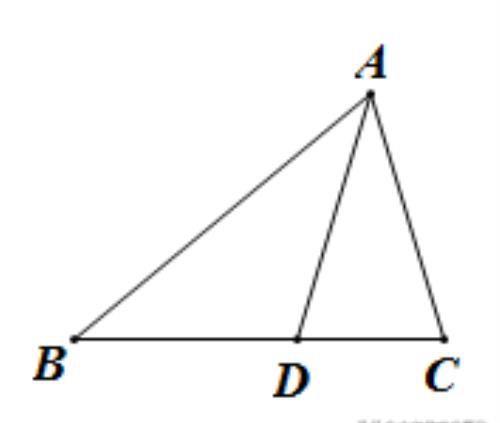
（2）如图，等腰△ABC和等腰△ABD中，AB=BC，BC=AD，当AB=AB，AD=AC，∠B=∠B时，△ABC和△ABD是伴生三角形，则AD=AC，∠B是伴生角．

∵BD=AD=AC，

∴∠B=∠BAD，∠ADC=∠C，

∴∠ADC=∠C=2∠B，

∵BA=BC，

∴∠C=∠BAC=2∠B，

在△ABC中，∵∠B+∠BAC+∠C=180°，

∴∠B+2∠B+2∠B=180°，

∴5∠B=180°，

∴∠B=36°．

【点睛】

本题考查了几何图形新定义，等腰三角形，三角形内角和，全等三角形等知识，根据题意理解好新定义并结合所学知识解题是解题关键．

19．（1）AB=CE+CD，见解析；（2）当点D在线段CB上时，AB=CE+CD；当点D在CB的延长线上时，AB=CD-CE,当点D在BC延长线上时，AB=CE-CD．

【分析】

（1）由对称可得DP垂直平分AE,则AD=DE,由∠ADP=30°可得△ADE是等边三角形,进而可得△ABC是等边三角形,可得AB=AC=BC，∠BAC=60°,进而可得∠BAD=∠CAE,由SAS可得△BAD≌△CAE,得BD=CE,进而可证得结论;

（2）数量关系又三种，可分三种情况讨论：①当点D在线段BC上时，（1）中已证明；②当点D在CB的延长线上时，如图所示，易知△ADE是等边三角形，可得AD=AE, ,由△ABC是等边三角形,可得AB=AC=BC，∠BAC=60°,进而可得∠BAD=∠CAE,由SAS可得△BAD≌△CAE,可得BD=CE,进而可得此种情况的结论；③当点D在BC延长线上时，如图所示，易知△ADE是等边三角形，可得AD=AE, ,由△ABC是等边三角形,可得AB=AC=BC，∠BAC=60°,进而可得∠BAD=∠CAE,由SAS可得△BAD≌△CAE，可得BD=CE,进而可得此种情况的结论.

【详解】

解：（1）AB=CE+CD

证明：∵点A关于射线DP的对称点为E，

∴DP垂直平分AE,

∴AD=DE,

又∵∠ADP=30°,

∴∠ADE=60°,

∴△ADE是等边三角形,

∴AD=AE，∠DAE=∠ADE=60°,

又∵△ABC是等边三角形,

∴AB=AC=BC，∠BAC=60°,

∴∠BAC-∠DAC=∠DAE-∠DAC,

即：∠BAD=∠CAE,

在△BAD和△CAE中,

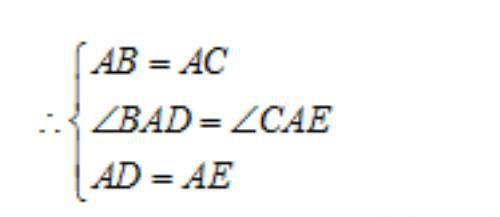
∴△BAD≌△CAE,

∴BD=CE,

∴AB=BC=BD+CD=CE+CD;

（2）AB=CE+CD，AB=CE-CD，AB=CD-CE.

①当点D在线段BC上时，AB=CE+CD,证明过程为（1）；

②当点D在CB的延长线上时，如下图所示，AB=CD-CE,证明过程如下：

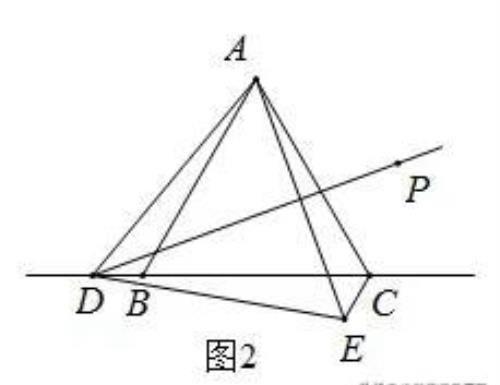
由（1）得，△ADE是等边三角形，

∴AD=AE, ,

又∵△ABC是等边三角形,

∴AB=AC=BC，∠BAC=60°,

∴∠BAC-∠BAE=∠DAE-∠BAE,

即：∠BAD=∠CAE,

在△BAD和△CAE中,

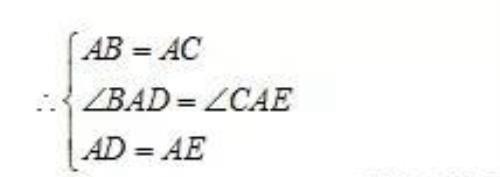
∴△BAD≌△CAE,

∴BD=CE,

∴AB=BC=CD-BD=CD-CE;

③当点D在BC延长线上时，如图所示，AB=CE-CD,证明过程如下：

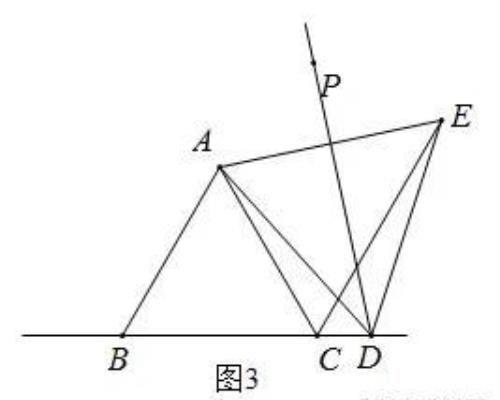
由（1）得，△ADE是等边三角形，

∴AD=AE, ∠DAE=∠ADE=60°,

又∵△ABC是等边三角形,

∴AB=AC=BC，∠BAC=60°,

∴∠BAC+∠DAC=∠DAE+∠DAC,

即：∠BAD=∠CAE,

在△BAD和△CAE中,

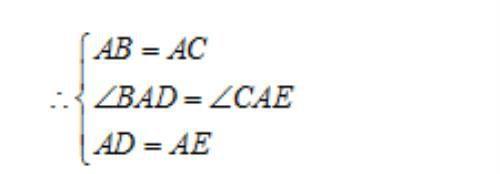
【点睛】

本题主要考查三角形全等的判定和性质，根据题目条件作出正确的图形找出全等的三角形是解题的关键.

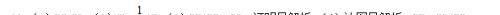
【分析】

（1）根据30°直角三角形的性质和中点的定义，即可得到答案；

（2）根据30°直角三角形的性质和中点的定义，证明△DBC是等边三角形，即可得到答案；

（3）同（2）的方法得出BC=BD进而得出△BCD是等边三角形，进而判断出△DCP≌△DBF，得出CP=BF即可得出结论；

（4）同（3）的方法得出BC=BD进而得出△BCD是等边三角形，进而判断出△DCP≌△DBF，得出CP=BF即可得出结论；

【详解】

（3）BF+BP＝BD，

理由：由（2）知△DBC是等边三角形，

∴∠CDB＝60°，DC＝DB，

∵线段DP绕点D逆时针旋转60°，得到线段DF，

∴∠PDF＝60°，DP＝DF，

∴∠CDB﹣∠PDB＝∠PDF﹣∠PDB，

∴∠CDP＝∠BDF，

∴△DCP≌△DBF，

∴CP＝BF，

∵CP+BP＝BC，

∴BF+BP＝BC，

∵BC＝BD，

∴BF+BP＝BD；

（4）如图③，BF=BD+BP，

∴△DCP≌△DBF，

∴CP=BF，

∵CP=BC+BP，

∴BF=BC+BP，

∵BC=BD，

∴BF=BD+BP．

【点睛】

此题是三角形综合题，主要考查了含30°的直角三角形的性质，等边三角形的判定，全等三角形的判定和性质，旋转的性质，解本题的关键是判断出△DCP≌△DBF，是一道中等难度的中考常考题．

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小曲创作整理编辑！