这题究竟有几种辅助线构造方式是什么(这题究竟有几种辅助线构造方式英语翻译)

导语：这题究竟有几种辅助线构造方式？

截长补短

遇到求证线段和差及倍半关系时，可以尝试截长补短的方法．截长指在长线段中截取一段等于另两条中的一条，然后证明剩下部分等于另一条；补短指将一条短线段延长，延长部分等于另一条短线段，然后证明新线段等于长线段．题目中常见的条件有等腰三角形（即两条边相等），或角平分线（即两个角相等），通过截长补短后，并连接一些点，构造全等得出最终结论．

【典型例题】——截长补短

例042．如图，点D为等腰直角三角形△ABC内一点，∠CAD＝∠CBD＝15°，E为AD延长线上的一点，且CE＝CA，则①DE平分∠BDC；②△BCE是等边三角形；③∠AEB＝45°；④DE＝AD＋CD，其中正确的有．

A．1个 B．2个 C．3个 D．4个

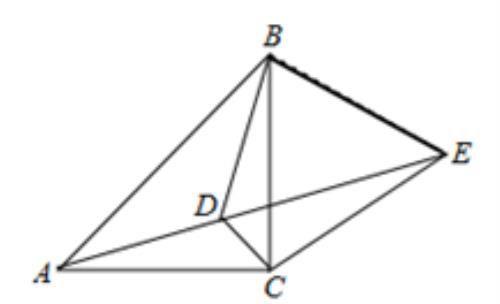
【解析】

解：（1）∵△ABC是等腰直角三角形，∠ACB＝90°，∴∠BAC＝∠ABC＝45°，

∵∠CAD＝∠CBD＝15°，∴∠BAD＝∠ABD＝45°－15°＝30°，∴BD＝AD，

∴D在AB的垂直平分线上，∵AC＝BC，

∴C也在AB的垂直平分线上，即直线CD是AB的垂直平分线，

∴∠ACD＝∠BCD＝45°，∴∠CDE＝∠CAD＋∠ACD＝15°＋45°＝60°，

∴∠BDE＝∠DBA＋∠BAD＝60°；∴∠CDE＝∠BDE，即DE平分∠BDC；

（2）∵CE＝CA，∴∠CAE＝∠CEA＝15°，由①得∠CDE＝60°，∠DCB＝45°，

∴∠BCE＝60°，∵AC＝BC，∴CE＝BC，∴△BCE是等边三角形；

（3）由②得△BCE是等边三角形，∴∠BEC＝60°，∴∠AEB＝∠BEC－∠CEA＝45°；

（4）【方法一】

如图1，在DE上取一点F，使得DF＝CD，并连接CF，

∵∠CDE＝∠BDE＝60°，∴∠BDC＝120°，△DCF为等边三角形，

∴∠DFC＝60°，DC＝FC，∴∠CFE＝∠CDB＝120°，

∵CB＝CE，∴△BDC≌△EFC，∴EF＝BD，

∴DE＝EF＋DF＝BD＋CD＝AD＋CD．

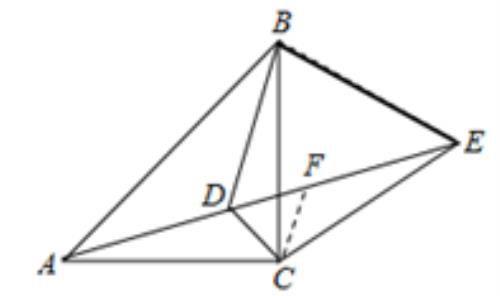
图1

【方法二】

图2

如图1，在DE上取一点F，使得DF＝AD，并连接BF，

证明△BDF为等边三角形，再证明△BFE≌△BDC即可．

【方法三】

如图3，延长DC至点F，使得CF＝AD，并连接EF，

∵AD＝DB，∴CF＝BD，∵等边△BCE，∴∠CBE＝∠BCE＝60°，BE＝CE，

∴∠DBE＝∠CBD＋∠CBE＝75°，∵∠BCD＝45°，∴∠ECF＝180°－∠DCE＝75°，

∴∠DBE＝∠ECF，∴△BDE≌△CFE，∴DE＝EF，

∵∠CDE＝60°，∴△DEF为等边三角形，∴DE＝DF＝DC＋CF＝AD＋CD．

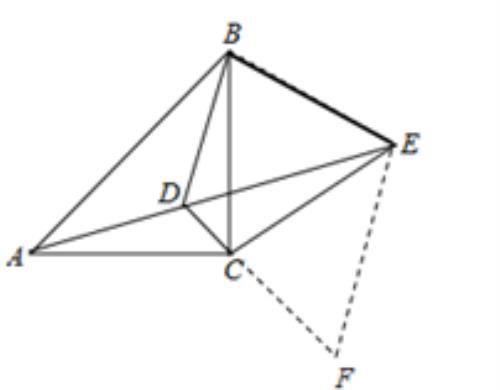
图3

【方法四】

如图4，延长DC至点F，使得DF＝AD，并连接AF，

证明△ADF为等边三角形，再证明△ACF≌△BDE即可．

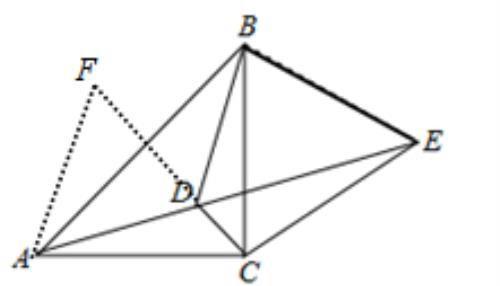
图4

【方法五】

如图5，延长DC至点F，使得DF＝AD，并连接BF，

证明△BDF为等边三角形，再证明△BCF≌△BDE即可．

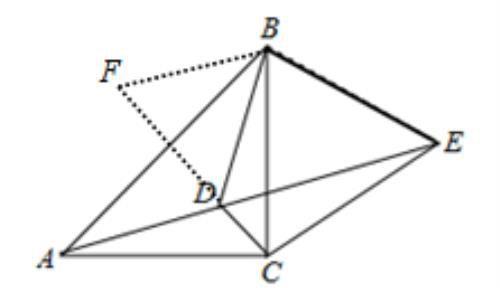
图5

【方法六】

如图6，延长BD至点F，使得DF＝DC，并连接CF，

证明△CDF为等边三角形，再证明△BCF≌△ECD即可．

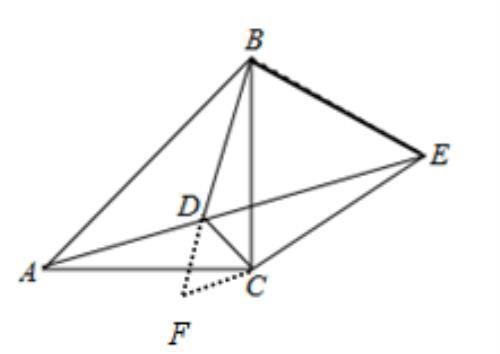
图6

【方法七】

如图7，反向延长BD至点F，使得BF＝DC，并连接EF，

证明△DEF为等边三角形，再证明△BEF≌△CED即可．

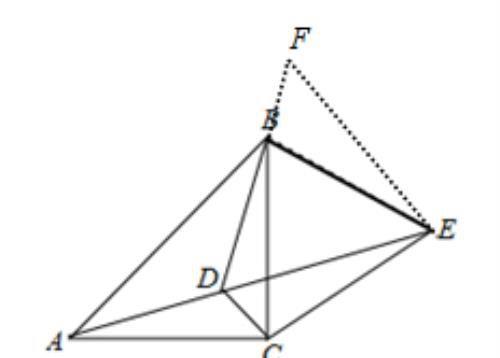
图7

…………

综上所述，结论①②③④都是正确的，答案选D．

【总结】线段和差的问题可以考虑使用截长补短的方法，在长的上面截取或者延长较短的线段，各种方法都可以尝试，并不一定全部可行，而且要注意辅助线的说明方式．本题第④个结论有多种角度出发可以证明，不知道各位同学还有什么其他的方法来证明吗？

当然，做选择、填空题的时候，我们只需要判断正确答案就可以了，并不需要严格的证明过程，但是这并不妨碍爱思考、爱动脑筋的同学，加油吧！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小薇创作整理编辑！