绝对值之和小值问题口诀(绝对值之和的大值)
导语:「初中数学-提高篇」绝对值之和的最值问题
在初中阶段,我们会遇到这样一类题目,求几个绝对值之和的最值问题。例如,求y=|x-2|+|x+2|的最小值,求y=|x-5|+|x+1|+|x+4|的最小值。这类问题,令许多同学感到棘手。今天,我们就详细剖析一下解决此类问题的方法,希望对同学们有所帮助。
首先,我们要明白绝对值的意义。|x|可以写为|x-0|,表示数轴上数x到原点的距离。|x-3|表示数轴上数x到3的距离。|x+3|可以写为|x-(-3)|,表示数轴上数x到-3的距离。对于|x+a|可以写为|x-(-a)|,表示数轴上数x到-a的距离。下面我们由简入难开始探讨。
一、y=|x+a|的最值问题
对于y=|x+a|,当x取任意实数时,y≥0。当x取有限范围时,我们如何解决呢?
例:对于y=|x+1|,分别求出下列情况时的最值。
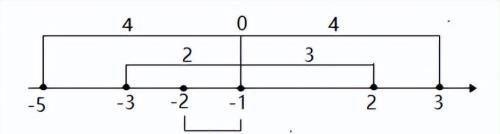
①当-5≤x≤-3时。②当-2≤x≤2时。③当x≥3时。
解法一、利用绝对值的意义
我们知道,y=|x+1|表示数轴上x点到-1的距离,那么通过数轴,我们可以很容易的解决此类问题。
①当-5≤x≤-3时,x到-1的距离最大值为当x=-5时的4,最小值为当x=-3时的2。故2≤y≤4。
②当-2≤x≤2时, x到-1的距离最大值为当x=2时的3,最小值为当x=-1时的0。故0≤y≤3。
③当x≥3时, x到-1的距离最大值不存在,最小值为当x=3时的4。故y≥4。
解法二、利用函数图像
我们可以采用数形结合的思想来解决此问题。首先,我们对y=|x+1|进行化简去绝对值如下:
绘出此分段函数图像如下:
然后将x的取值范围标在图像上,如下所示:
根据函数图像,我们也可以很容易得到三种情况下y的最值问题。
二、y=|x+a1|+|x+a2|(a1≠a2)的最值问题
例:求y=|x+1|+|x-1|的最值,此时x可以取任意实数。
解法一、利用绝对值的意义
y=|x+1|+|x-1|,表示数轴上x点到-1和1的距离之和。首先,我们画出数轴。
根据上图,我们可以总结如下:
①当x<-1时,x点到-1、1的距离之和最小值为当x=-1时的|-1+1|+|-1-1|=2,最大值不存在。故y>2。
②当-1≤x≤1时,x点到-1、1的距离之和为固定值2,也就是点1到-1的距离。故y=2。
③当x>1时,x点到-1、 1的距离之和最小值为当x=1时的|1+1|+|1-1|=2,最大值不存在。故y>2。
也就是说对于y=|x+1|+|x-1|,当-1≤x≤1时,y有最小值,最小值就是数轴上点1到-1的距离2。
同理,我们可以推出一般式y=|x+a1|+|x+a2|的最值问题。它的意义是数轴上x点到-a1和-a2的距离之和。它的最值是当-a1≤x≤-a2 (假设a1>a2)时,y有最小值,最小值就是数轴上-a2到-a1的距离|-a2-(-a1)|=|a1-a2|。
解法二、利用函数图像
首先,对y=|x+1|+|x-1|化简去绝对值如下:
绘出此分段函数图像如下:
通过此图像,我们也可很容易的得到y=|x+1|+|x-1|的最值问题。并且与利用绝对值得到的结论相同。
解法三、 利用不等式知识
根据解法二中化简后的函数,我们可以利用不等式的知识来解决,例如,当x<-1时,y=-2x>2。当x>1时,y=2x>2。
三、y=|x+a1|+|x+a2|+|x+a3|( a1、a2、a3互不相等)的最值问题
例:求y=|x+1|+|x-1|+|x-2|的最值,此时x可以取任意实数。
解法一、利用绝对值的意义
y=|x+1|+|x-1|+|x-2|,表示数轴上x点到-1、 1和2的距离之和。首先,我们画出数轴。
根据上图,我们可以总结如下:
①当x<-1时,x点到-1、 1和2的距离之和最小值为当x=-1时的|-1+1|+|-1-1|+|-1-2|=5,最大值不存在。故y>5。
②当-1≤x≤1时,x点到-1、 1的距离之和为固定值2,那么x点到-1、 1和2的距离之和为2加上点x到2的距离。显然x点到2的距离最大值为当x=-1时的|-1-2|=3, 最小值为当x=1时的|1-2|=1。故3≤y≤5。
③当1<x≤2时,x点到1、 2的距离之和为固定值1,那么x点到-1、 1和2的距离之和为1加上点x到-1的距离。显然x点到-1的距离最大值为当x=2时的|2+1|=3, 最小值为当x=1时的|1+1|=2。故3<y≤4。
④当x>2时,x点到-1、 1和2的距离之和最小值为当x=2时的|2+1|+|2-1|+|2-2|=4,最大值不存在。故y>4。
也就是说对于y=|x+1|+|x-1|+|x-2|,当x=1时,y有最小值,最小值就是数轴上点2到-1的距离3。
同理,我们可以推出一般式y=|x+a1|+|x+a2|+|x+a3|的最值问题,它的意义是数轴上x点到-a1、-a2和-a3的距离之和。它的最值是当x=-a2 (假设a3<a2<a1)时,y有最小值,最小值就是数轴上-a3到-a1的距离|-a3-(-a1)|=|a1-a3|。
解法二、利用函数图像
首先,对y=|x+1|+|x-1|+|x-2|化简去绝对值如下:
绘出此分段函数图像如下:
通过此图像,我们也可很容易的得到y=|x+1|+|x-1|+|x-2|的最值问题,即当x=-1时,y有最小值3。
解法三、 利用不等式知识
此方法不再赘余,希望同学们自己加以研究。
四、y=|x+a1|+|x+a2|+……+|x+an|( a1、a2、……、an互不相等)的最值问题
根据以上三种情况的剖析,我们可以推及到n个绝对值之和的最值问题,它们具有以下规律:
根据绝对值的意义,y表示数轴上x点到点-a1、点-a2、……、点-an的距离之和,首先,将这些点一一标注在数轴上,然后分以下两种情况解决。
1绝对值的个数为奇数时(n为奇数)
当x等于数轴上这n个点(从小到大排列)的中间那个点的值时,y有最小值,求最小值时,我们可以把这个数代入|x+a1|+|x+a2|+……+|x+an|即可。例如:y=|x+1|+|x+2|+|x+3|+|x-4|+|x-5|,表示x到-1,-2,-3,4,5的距离之和,当x取-3,-2,-1,4,5(从小到大排列)中间这个点-1时,y有最小值。最小值为y=|-1+1|+|-1+2|+|-1+3|+|-1-4|+|-1-5|=14。但y不存在最大值。
2绝对值的个数为偶数时(n为偶数)
当x取数轴上这n个点(从小到大排列)的中间两个点之间的任意值时,y有最小值,求最小值时,我们可以在这两个点之间任意取一个值,把它代入|x+a1|+|x+a2|+……+|x+an|即可。例如:y=|x+1|+|x+2|+|x+3|+|x-4|+|x-5|+|x-8|,表示x到-1,-2,-3,4,5,8的距离之和,当x取-3,-2,-1,4,5,8(从小到大排列)中间两个点-1和4之间任意一个数时(即-1≤x≤4),y有最小值。我们可以取其中任意一个数,例如0,代入式中求出最小值为y=|0+1|+|0+2|+|0+3|+|0-4|+|0-5|+|0-8|=23。但y不存在最大值。
通过以上分析,我们总结出了求此类问题最值的规律,利用此规律,同学们可以很轻松的解决此类问题。但最重要的是希望同学们遇到问题时善于思考,勤于总结,这对同学们以后的学习会大有裨益。
本文内容由小姬整理编辑!