全体自然数之和竟然等于-1/12这个结果是什么(全体自然数之和等于多少)

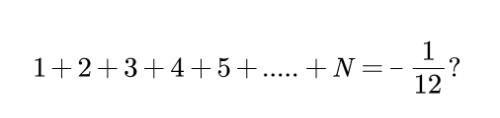
导语：全体自然数之和竟然等于-1/12？这个结果究竟是对还是错？

我们来探讨这样一个奇怪的问题，相信大家都见过下面这个等式：

它究竟是对还是错呢？话不多说，就让我们开门见山。

卡西米尔效应

不提解析延拓就谈自然数之和为负数，简直是“耍流氓”

在通常的研究范畴中，这个和是不存在的，就算是没有受过教育的人也能认识到，无穷多个正数相加，怎么可以出现负数呢？

自然数之和的通项公式长这样子：

可为什么仍然有人认为下面的公式成立呢？

我们必须在此强调，求一个无穷数列和的必要条件是——该无穷数列必须收敛。而1+2+3+...n显然是发散的，是不能求和的。（如何判断无穷级数的敛散性，请看笔者之前的文章，里面有详细论述）

市面上流行的简单证明方法是错误的

我们来看看一种错误的证明，虽然它可以算出1+2+3+...n等于-1/12，然而毫无意义。不声明适用范围的“推导”在数学上是非法的，无意义的，即使它碰巧结果对了。

（这里只写一部分，详细过程就不啰嗦了，因为全篇的“证明”思路同这部分大同小异），然后分析一下它为什么错了：

我们假设下面这个和存在，记为A，则：

把小括号去掉：

前两项 1 - 1 的结果显然为0，上式就变成：

接下来的技巧和列等号就已经是错的了,继续写下去毫无意义，因为该数列本就是发散的，本来就不能对一个发散的数列求和。

具体“证明”过程笔者不再赘述。相信大家已经看出来了，A=1-1+1-1...自然是发散数列，是不能求和的，想当然的给它赋予1/2，这就是错误的地方（如果按照类似的方法去处理，还可以得到A=0）

让我们来看一种正确的证明方法：

既然你说“1+2+3+4+.......n等于-1/12”是错误的，那为什么它又是“对”的呢？原因就在于我们提前声明这个结果成立的前提条件，适用范围是什么：只有在解析延拓（Analytic continuation），也就是在复变函数体系下，才能认为上面的结果是正确的。

解析延拓

如何通俗理解解析延拓呢？原来的求和只能在发生在实数域上，而现在实数域的基础上将复数域按照光滑的性质杂糅耦合进来了，也就是将实数域扩充到复数域上了（多出来了虚数轴）：

现在开始证明它，我们需要准备两大数学工具——部分黎曼ζ函数和巴塞尔级数：

先说黎曼Zeta函数：

黎曼zeta函数

它长什么样子呢？它实际上涵盖了整个复平面负半轴，函数线上的点代表了复数坐标（x，yi）

式中Γ（s）为伽马函数

伽马函数

我们还要知道一个重要级数求和式，它是由欧拉最早证明的（巴塞尔问题）：

它的证明过程本文就不多叙述了。我们只需拿过来用一下。

知道了这些，我们要想证明1+2+3+4+.......n等于-1/12，实际上就是在求ζ（-1）的值究竟是多少，为什么呢？因为ζ（1）所代表的是：

所以：

而：

代入可得：

这才是1+2+3+4+.......n等于-1/12的来历。

黎曼

拉马努金的手稿

本文内容由小萱整理编辑！