一元函数的导数例题(一元函数导数的含义)

导语：每日一题 数学 第三章 一元函数导数及其应用 P3

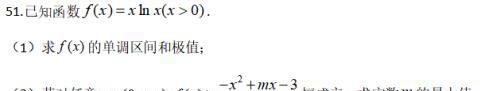
解析

20.4 函数极值与最值：

1．函数的极值(1)函数的极小值：函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；而且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0，则点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．

(2)函数的极大值：y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；且在点x＝b的左侧f′(x)＞0，右侧f′(x)＜0，点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．极小值点、极大值点统称为极值点，极大值和极小值统称为极值.注：①函数f(x)在x0处有极值的必要不充分条件是f′(x0)＝0，极值点是f′(x)＝0的根，但f′(x)＝0的根不都是极值点 (例如f(x)＝x3，f′(0)＝0，但x＝0不是极值点).②极值反映了函数在某一点附近的大小情况，刻画的是函数的局部性质.极值点是函数在区间内部的点，不会是端点.

2．函数的最值(1)在闭区间[a，b]上连续的函数f(x)在[a，b]上必有最大值与最小值．(2)若函数f(x)在[a，b]上单调递增，则f(a)为函数的最小值，f(b)为函数的最大值；若函数f(x)在[a，b]上单调递减，则f(a)为函数的最大值，f(b)为函数的最小值

3.导数与零点、不等式：(1)导数零点：可构造函数，将俩曲线交点问题转化为函数零点问题。(2)不等式(恒成立)：分离参数。构造函数。分类讨论。转化为函数最值问题。

4.常用结论(1)对于可导函数f(x)，“f′(x0)＝0”是“函数f(x)在x＝x0处有极值”的必要不充分条件.(2)求最值时，注意极值点和所给区间的关系，关系不确定时，要分类讨论，不可想当然认为极值就是最值.(3)函数最值是“整体”概念，而函数极值是“局部”概念

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小曲创作整理编辑！