导语：智慧笔记：芝诺悖论——竟以“极限”之名令辩证法熠熠生辉？

作者|公子小白

【愿哲学被听见】公子小白继续和您一同寻找西方哲学的踪迹。

哲学家芝诺

芝诺是巴门尼德的学生，他的鼎盛时期大约在公元前468年前后。芝诺曾经就伊奥尼亚学派有关变化的世界本源观念，提出了举世闻名的四个著名论证。但事实上，芝诺的观点因过度极端，与其说是对其恩师巴门尼德思想的延续，倒不如说，芝诺旨在维护巴门尼德有关真理学说的层面上，采用了矫枉过正的做法。

柏拉图的注说

沉思的芝诺

后来，在柏拉图所著的《巴门尼德篇》中，曾经指出，他们采用了“以彼之道，还施彼身”的辩护策略：有的人指责说，倘若“存在是不变的一”予以承认，那么，所得出的荒谬结论必然是“事物不能运动”；此时，他们则反驳，如果对存在之变化予以承认，如此一来，事物不能运动的结论同样以此推到而出，并且，这将成为矛盾与前提的悖论，岂不是更加荒谬？

芝诺悖论

1.二分法：

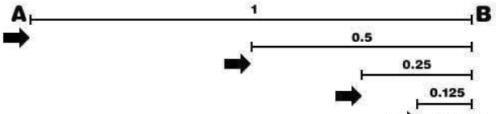
二分法悖论

任何运动的事物，早在其抵达目的地之前，需要事先完成它的全程；在达到1/2之前，需要事先完成其1/2；在达到其1/4之前，则事先完成其1/4……。如此无限分割，直至无穷，因此它将无限趋近于目的地却始终难以达到目的地。

2.阿基里与乌龟赛跑：

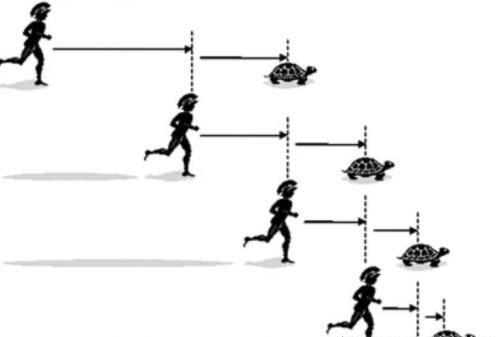
阿基里与乌龟赛跑

我们假设古代奥林匹克赛跑冠军阿基里与一只乌龟进行一场赛跑比赛，乌龟首先爬行了一段路程；当阿基里开始起步并同样跑完这段路程之后，乌龟又再次向前爬行一段路程；当阿基里跑完这有一段路程后，乌龟又再一次向前爬行了一段路程；如此一来，一爬以追，无限往复，赛跑冠军将永远不可能追上这只缓慢爬行的乌龟。这则阿基里与乌龟赛跑的悖论向人们证明，运动着的事物并无快慢可言。

3.飞矢不动：

飞矢不动

我们想象一下，一个飞矢在一段时间内所飞过的路程，其中可以被切割成无数个时刻或瞬间。而在每一个瞬间，飞矢都占据着一个孤立的位置，那么，在每一个位置上的飞矢则是静止不动的。换句话说，飞矢实际上是驻留在整个路程的每一个不同的位置之上，而非从一个位置飞到另外一个位置。

4.一倍的时间等于一半的时间：

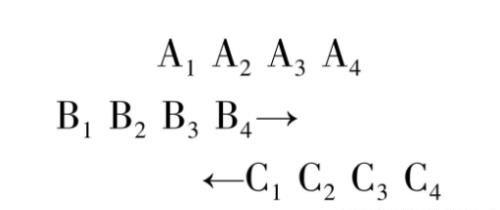
一倍的时间等于一半的时间悖论

如上图↑，我们来假设B和C两组系列字母所运动的速度相同且方向相反，A、B、C三组系列字母的每个部分的大小、质量都完全相同。那么，B4抵达A4的时间，则势必与C1抵达A1的时间相同。

但是，由于相对于A系列字幕，B系列字幕仅仅移动了两格，因此其运动时间则是相较于C系列字幕运动时间的一半。也就是说，C系列字幕相对于B系列字幕移动了四格，所以C系列字母运动的时间要足足比B系列字母的运动时间多出了一倍。这么一来，本应相等的时间却出现了倍数的差别，这便是“一倍时间等于一半时间”的悖论。

无穷

在芝诺的四个悖论中，除了第四个“一倍时间等于一半时间”悖论外，其他三个悖论的内容均适用于收敛数列。因此，“二分法”可以以现代数学符号表示为1，1/2，1/4，1/8，1/2n（n趋向无穷大）的数列。

对芝诺悖论的评价

尽管通过现代数学的论证不难解释芝诺所提出的上述悖论的谬误，但他们绝不仅仅是简单意义上的“诡辩”，其后蕴藏着的哲学意义形成了对后世的巨大启示。可以说，芝诺通过有关运动的数学分析，历史性地使用了微积分运算，并将其见诸在“极限”的概念之上，也正是对“极限”的使用，承认了无限与有限，连续与间断的相互统一。而以上这些，都是数学所无法予以正面的证明和解答的。“极限”作为数学领域最基础的概念，却不能被数学本身加以解释，需要进一步诉诸更为严谨的现代逻辑与数学哲学。

芝诺

可以说，芝诺延续了古希腊哲学家们的思辨风格，并率先运用悖论的方式对提出哲学诘难。通过悖论，将有限和无限、连续和间断、整体和部分的对立与统一呈现在哲学面前，进一步深化了早期自然哲学关于一与多，流变与永恒之间的反思。基于芝诺悖论的哲学魅力，他被后来的亚里士多德誉为“辩证法的创始者”。

关注我，不迷路，没错的！

更多日常交流、思想碰撞！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑！